Are Price to Revenue and Price/Earnings Valuation Methods Really Independent Valuation Methods?

Views Developed by an Appraiser Working with Business Brokers to Assess FMV

Business appraisers typically assume that Price/Revenue, Price/SDE, Price/EBITDA and Price/EBIT, etc., are independent valuation methods. But, are they independent? This article shares my views on this subject matter and why they will lead to different conclusions of value.

[su_pullquote align=”right”]Resources:

The Three Valuation Approaches—Challenges and Issues

How to Effectively Use Market Data in Your Valuation Reports

EBITDA Single Period Income Capitalization for Business Valuation

Business Valuation Certification and Training Center

[/su_pullquote]

Business appraisers typically assume that Price/Revenue, Price/SDE, Price/EBITDA and Price/EBIT, etc., are independent valuation methods.  But, are they independent?  This article shares my views on this subject matter and why they will lead to different conclusions of value.

First, I believe and think that it is not argued, that Revenue, Seller’s Discretionary Earnings[1] (SDE), EBITDA, and EBIT, Gross Profit Margin, etc., are related to each other.  This suggests that these are not independent of each other.

First, consider the relationship between Price/Revenue and Price/SDE.  In this article, I am only discussing those businesses that are purchased and/or valued based on earnings, not on synergies or other variables.  In this scenario, it is usually assumed that the Price/SDE multiple is the independent variable and the Price/Revenue multiple is the dependent variable.  The reasoning for this is that intuitively we know that the Price/Revenue multiple needs to be adjusted for the subject’s profitability, i.e., in practice, I believe that the Price/Revenue multiples tends to over value low profitability companies and tend to undervalue highly profitable companies if they have the same revenue.

The following illustrates the above observation and view:

Subject Company 1:

• Revenue = $4,000,000
• SDE = $500,000
• EBITDA = SDE – Owner’s Comp = $300,00
• Owner’s Comp = $200,000
• Sales Price = $1,750,000

From the above data, we can calculate the various pricing multiples:

• Price/Revenue = 0.4375
• Price/SDE = 3.5000
• Price/EBITDA = 5.83333
• SDE/Revenue = 0.1250

The calculations were carried out to four significant figures to minimize rounding errors for demonstration purposes only.  By definition, each of the above pricing multiples gives the same value for the subject.  For this situation, the relationship between the Price/Revenue and the Price/SDE multiples can be derived as follows:

(Price/Revenue)_Multiple x Revenue_Subject = Value

(Price/SDE)_Multiple X SDE_Subject = Value, therefore,

(Price/Revenue)_Multiple x Revenue_Subject = (Price/SDE)_Multiple X SDE_Subject

Rearranging terms gives:

(Price/Revenue)_Multiple = (SDE_Subject/Revenue_Subject) x (Price/SDE)_Multiple                        Equation 1

Equation 1 describes a straight line through the origin with a slope of SDE/Revenue.  This equation indicates that for businesses purchased/valued based on earnings, the Price/Revenue multiple is equal to the subject’s profitability, i.e., SDE/Revenue, times the Price/SDE multiple.

For the assumed transaction, Price/Revenue = SDE/Revenue x Price/SDE = .125 x 3.5 = .4375, this is the same as the Price/Revenue multiple calculated using the transaction variables.

Again, by definition, this method of calculating the Price/Revenue multiple gives the same value indication for the subject transaction.  The question now is, what does this mean when valuing a subject company?

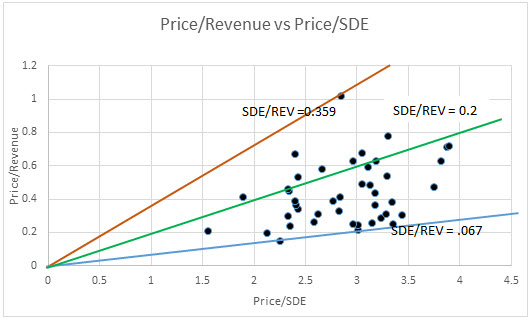
One way to answer this question is to plot the comparables data as shown on Figure 1 below.

On the Figure, we have plotted the Price/Revenue multiple versus the Price/SDE multiple using actual comparables data (See Appendix for Comps Data).

 

The data in the Appendix shows that the maximum value of SDE/Revenue (SDE % in the Appendix) is 0.359 and the minimum value is 0.67.  It can easily be shown that the slope of the orange line is equal to the maximum SDE/Revenue ratio and the Slope of the blue line is equal to the minimum SDE/Revenue ratio (See the comps data in the Appendix).  This means that every data point falls on a straight line that goes through the origin with a slope equal to the SDE/Revenue value for that data point.  This situation is obvious from Equation 1.

This means that the dispersion in the comparables data is due to the dispersion in profitability of the comparable companies.  It also indicates that a tight distribution, i.e., R² approaching 1.0, does not mean that there is high confidence in the Price/Revenue multiple unless the comparable companies have profitability the same as or similar to that of the subject company.  It also means that the coefficient of variation is not necessarily meaningful for the price/revenue multiple unless the comparable companies have profitability like that of the subject company.

This also implies that if all the comparable companies have the same profitability as the subject company, the values based on the Price/SDE method and the Price/Revenue method determined using linear regression (by plotting Sale Price vs. SDE, and, Sale Price vs. Revenue) would be the same.

For example, assume that we have the following subject company with SDE/Revenue = 0.2 corresponding to the green line on the chart.

Subject Company 2:

• Revenue = $2,500,000
• SDE = $500,000
• SDE/Revenue = 0.2
• Price/SDE = 3.0
• Value = 3.0 x $500,000 = $1,500,000

With the subject’s Price/SDE multiple =3.0, the Price/Revenue multiple determined from the green line on the chart, which matches the subject company’s profitability, would be 0.2 x 3.0 = 0.6.  This would give a value indication of $1,500,000, which is the same as for the Price/SDE multiple.

If we determine the Price/Revenue multiple from the orange curve (i.e., if all comparables fall on, or close to this line), which corresponds to higher profitability than that of the subject, the Price/Revenue multiple would be 1.077.  This multiple gives a value indication of $1,392,758 x 1.077 = $2,682,500.  This significantly overvalues companies with lower profitability.

If we determine the Price/Revenue from the blue line for which SDE/Revenue = 0.067 (i.e., if all comparables fall on, or close to this line), the Price/Revenue multiple would be 3.0 x 0.67 = 0.2 and the value indication would be $502,500, which, significantly undervalues the higher profitability subject company.

These results indicate once again that if all the comparable companies have the same profitability as the subject company, the Price/SDE and Price/Revenue multiples determined graphically would give the same value indications.  This result also indicates that the Price/SDE multiple and Price/Revenue multiple are not independent; and, that Equation 1 applies.  In summary, the Price/Revenue multiple should give the same value as the Price/SDE multiple, and, therefore it does not provide any additional information regarding the value of the subject.

Using the same methodology described above, one can determine the relationship between the Price/SDE multiple and the Price/EBITDA multiple (and any other multiple for that matter).  Again for businesses purchased/valued based on earnings; and, assuming that Price/SDE is the independent variable and Price/EBITDA is the dependent variable, the relationship is given by the equation, developed below:

Since by definition, for each comparable transaction, the Price/EBITDA and Price/SDE multiples give the same value, one can write:

(Price/SDE)_Multiple x SDE_Subject = Value

(Price/EBITDA)_Multiple x EBITDA_Subject = Value

Since the above equations both equal Value, the two equations can be set equal to each other:

(Price/EBITDA)_Multiple x EBITDA_Subject = (Price/SDE)_Multiple x SDE_Subject

Rearranging terms, and dividing by EBITDA, one obtains the following:

(Price/EBITDA)_Multiple = (SDE_Subject  / EBITDA_Subject) x (Price/SDE)_Multiple

Substituting SDE – Officer Comp for EBITDA gives:

(Price/EBITDA)_Multiple = (SDE_Subject / (SDE_Subject – Officer’s Comp)) x (Price/SDE)_Multiple

Dividing through the numerator and denominator of the right side of the above equation by SDE gives:

Price/EBITDA_Multiple = 1 / (1 – Owner’s Comp/SDE_Subject) x Price/SDE_Multiple    Equation 2

Equation 2 assumes that the Price/SDE multiple is the independent variable and the Price/EBITDA is the dependent variable.  The reasoning for this is that EBITDA has one more variable than SDE, i.e., the owner’s compensation (EBITDA = SDE – Owner’s Comp).

Equation 2 describes a straight line through the origin with a slope = 1 / (1 – Owner’s Comp/SDE).

Analyzing the relationship between Price/EBITDA multiples and Price/SDE multiples, one will come to the same conclusions reached for Price/Revenue and Price/SDE multiples.  That is, they are not independent of each other and, they should both give the same value indication.

In summary, for businesses purchased/valued based on earnings one need only consider the Price/SDE valuation method in the Market Approach.  When correctly determined, the other methods do not add any additional information.

The same approach can be used to analyze the relationship between price/revenue and price to earnings multiples for small service businesses that tend to be purchased/valued based on revenue.  In this situation, the Price/Revenue multiple would be the independent variable and the Price/Earnings multiple would be the dependent variable.

Please click here to see the attached Appendix for the comps data.

[1] SDE = Pre-Tax Net Income plus non-recurring and non-operating expense less non-recurring and non-operating income plus non-cash expense (i.e., depreciation and amortization).

Wayne Quilitz, CTEP, CMEA, is President of Murphy Valuation Services, LLC, a Clearwater, FL advisory services firm affiliated with Murphy Business & Financial Corporation.
Mr. Quilitz can be reached at (727) 725-7090 or by e-mail to wquilitz@murphybusiness.com.