The Size Effect Continues to be Relevant
Criticism of Ang (Part II of III)
In the second part of this three-part article, Roger Grabowski respond to criticism over the years about the validity of CRSP Decile Size premia data. He begins by addressing the criticisms from a paper published in NACVA’s QuickRead by Clifford Ang. Roger Grabowski argues that Ang’s critique is flawed and presents concrete evidence to that effect. He also addresses other criticisms that have been made about size premia.

[su_pullquote align=”right”]Resources:
The Size Effect—It is Still Relevant
The Three Valuation Approaches—Challenges and Issues
Size Premium: Seductive Siren or DOA
[/su_pullquote]
In the second part of this paper, I would like to respond to criticism over the years about the validity of size Premia. I will start by addressing a paper published in NACVA’s QuickRead by Clifford Ang.[1] Ang advocates that the CRSP Decile Size Premia (SP) reported as calculated by Duff & Phelps is erroneous. I will explain how his logic is flawed and present concrete evidence to that effect.
Criticism: Size Premium is an Error in a Statistical Sense
Ang considers SP nothing but an excess of return that is not captured by the CAPM and added back labeled a Size Premium. The author refers to the size premium as an “error” in a statistical sense. However, none of the academic papers throughout the last three decades have qualified the SP as a statistical error. The harshest criticism of SP amounted to its inability to represent an actual risk but merely related to firm characteristics, hence the stability of the premium over time. This criticism started with Daniel and Titman[2] and continued as the major concern about adopting Professors Eugene Fama and Kenneth French’s (F-F) Small Minus Big (SMB) as a factor for pricing assets.
The author refers to data mining, which is not a statistical error per se. Data mining is finding an empirical relationship that could not hold in all data samples. The fact that SP is possibly obscured over a certain period by other factors does not negate its existence. The question that academics and other researchers are asking is why it exists over a period and not another, and what is the economic logic behind it. Asness et al. argue that all the challenges to SP disappear and it becomes stable over time when controlling for firm quality in 24 international equity markets and 30 industries.[3]
Another explanation for the use of the phrase “statistical error” by the author, is his concern about the possibility that SP captures idiosyncratic components of individual firms that do not have any systematic pricing capability. Calculations of the SP requires the use of a portfolio of firms precisely to avoid being hijacked by the idiosyncratic components of individual members of the portfolio. Hence, when SP is calculated, it would refer to the additional return required by the holder of a typical (average) firm in that portfolio typical size (or decile), not a specific individual firm.
Duff & Phelps’ calculations of the SP in the CSRP Decile Size Study are based on large portfolios of firms diversifying all idiosyncratic risk of individual firms. The number of companies in the size portfolios is high enough to diversify the nonsystematic risk. For example, the historical average number of stocks in the lowest CRSP decile is around 1,300 firms with a low of 50 in the 1920s and a high of 3,575 in 1997. The historical average number of stocks in the highest CRSP decile is 124 with a low of 50 in the 1920s and a high of 124 stocks in 2000. These high numbers largely exceed the number of stocks required to diversify idiosyncratic risk in a portfolio of around 40.[4]
The expected return of a portfolio using MCAPM is:
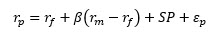
As the number of stocks in the portfolio p increases, the value of goes to zero. Because, the number of stocks in all CRSP deciles is more than fifty, we can confidently say that is:
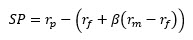
and it does not contain any idiosyncratic components of individual stocks.
Criticism: Duff & Phelps Size Premia Are Biased
Ang argues that SP does not match how valuation professionals calculate betas. His argument assumes that size factor is conditional on short-term movement of stock returns and should be adjusted to reflect recent information. This reasoning could be right if we knew exactly what “risk” the size factor represents. In the case of beta (market risk) for example, a time interval of five years is commonly used for the look-back period over which beta is estimated to reflect the market risk profile of the firm during a typical economic cycle. Originally it was thought that beta was unconditional (i.e., time invariant) until Jagannathan and Wang (1996) proved that it needs to be time variant to work.[5] Other research has shown that monthly returns measured over longer look-back periods provided a more reliable estimate of subsequently observed betas, particularly betas for small cap companies.[6]
How is the “Practitioner Consistent Size Premium” Different?
Ang argues for a new methodology to calculate the SP dubbed “Practitioner Consistent Size Premium” (PCSP). His methodology purports to remove the bias and what he perceives as errors in estimating the SP.
The author’s methodology does not provide an original way of calculating the premium and it is essentially the same as what is found in Cost of Capital: Applications and Examples 5th ed. and in the Duff & Phelps Valuation Handbook—U.S. Guide to Cost of Capital.[7] His methodology is a mere change in the length of the look-back period used to estimate the betas of the portfolios (three years) and the period to calculate market, portfolio, and risk-free returns (twelve months). The use of different time periods for the calculation of beta, returns, and Equity Risk Premium (calculated over a minimum period of thirty-five years) induce an inconsistency in the estimates and, of course, leads to numbers with no meaning. The author’s methodology is outlined as follows:
- Calculate the excess return of each decile portfolio as the difference between the twelve-month period return and the cumulative risk-free return over the same twelve-month period.
- Estimate the beta for each decile using monthly returns for three years.
- Calculate the historical equity risk premium (ERP) for the period from 1926 to the current year. The earliest estimate of the PCSP should be for 1961 to guarantee at least thirty-five years of data of the ERP.
- Calculate the expected return as beta multiplied by ERP.
- PCSP is the difference between the twelve-month realized return calculated in step 1 and the expected return calculated in step 4.
In short, the PCSP use the same equation as the SP: where and are calculated over the last twelve-month period and over the three-year look-back period and is the historical ERP since 1926. These inconsistencies between the dates used for the calculation of PCSP render it useless because it does not really capture the actual SP, but a deviation of the return from a long-term expectation using a short-term estimated beta.
Estimation Issues in PCSP
Valuation professionals use cost of capital to discount projects with long-term life spans. The only logical thing is to use long-term estimates of the cost of equity, and for the SP as well. The use of three years and twelve months to calculate the alternative SP is inconsistent.
The author argues that using a three-year period for estimating beta of different portfolios based on size (i.e., deciles) is more appropriate because it reflects the up-to-date information. However, the choice of the estimation period depends on the objective of the estimation. As we pointed out above, research has shown that using a longer look-back period provides a more reliable beta estimate, particularly for small cap firms of 250 days.
In the case of SP, we are estimating a “risk premium”[8] to be used to discount cash flows of projects with long-term life spans. We need to estimate a stable and long-term market risk premium, which implies the need for a long enough period of estimation. The author is contradicting himself when he is using an ERP of a minimum thirty-five years and expanding his window; and assumes that the SP should be calculated using twelve-month returns and a relatively short estimation window.[9] The three-year look-back period is too noisy for estimating beta, and it picks up short-term variation in the portfolio returns.
To illustrate, I estimated betas for both large and small firm deciles using returns from Professor Kenneth French’s website.[10] I calculated monthly beta following the methodology proposed by Ang (three-year look-back period) and monthly betas using an expanding window as it is done in Duff & Phelps Valuation Handbook. The results are plotted in Figure 1. The moving three-year estimation period proposed by Ang is noisy and shows that betas of small cap stocks fluctuate between a low of 0.58 and a high of 1.7; where betas estimated using an expanding window from 1926 to current has a low of 1.42 and a maximum of 1.64. This means that a portfolio of small firms with a beta of 0.58 has an expected return of 48% lower than the market portfolio. Does this mean that a portfolio of small cap stocks is a defensive portfolio?
Figure 1: Low and Large Size Portfolios’ Betas
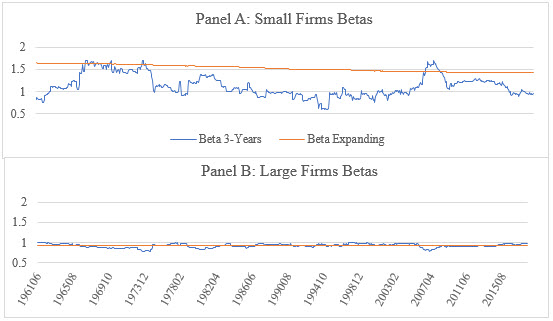
The graph depicts estimates of beta over the period 1961:06 to 2018:06 using a three-year moving look-back period and an expanding look-back period starting 1926:06 for low and large size portfolios.
Imagine that a Chief Financial Officer is using this methodology to calculate the net present value (NPV) of a project with the same size as a firm in the lowest decile. The obtained required rate of return would be nearly half what would be expected from the market portfolio and possibly resulting in accepting projects that should be rejected. The estimates of the three-year look-back beta are affected by market conditions which makes estimating the long-term expected return of CAPM impossible. These movements are temporary and would bias our estimates of a long-term cost of equity for a long-term project, or simply for a company with indefinite life. While using a short look-back period may be useful for day traders, valuation professionals are typically estimating underlying value based on long-term prospects. The methodology the author is proposing is picking up the statistical errors that he was set to avoid by proposing the same methodology.
The volatility of the PCSP estimate increases even further with the proposed use of the twelve-month period in calculating return of small cap and large cap portfolios and the return of a riskless asset. Choosing a twelve-month period does not represent a good proxy for long-term returns of the portfolios. The objective of the author is to have returns that reflect the current market conditions, but these are not market conditions that will prevail in the future and one should be careful when engaging in this exercise.
Other Criticisms
Risk Premium Report Results Embody Hindsight
Other critics have suggested that the returns reported in the Risk Premium Report are the result of embodying hindsight. All categorization of companies for the Risk Premium Report dataset and portfolios is based on data known before the beginning of each year for which returns are calculated.
In determining companies to exclude from the base dataset (e.g., companies lacking five years of publicly traded price history or companies with a negative five-year average EBITDA for the previous five years), all data for the selection process are known before the beginning of any year. The exclusion of companies based on historical financial performance does not imply any unusual foresight on the part of hypothetical investors in these portfolios. In forming portfolios to calculate returns for a given year, we exclude companies on the basis of performance during previous years (e.g., average net income for the five prior fiscal years), rather than current or future years. Portfolio ranking based on size characteristics in the Risk Premium Report—Size Study are always determined by size measures preceding the annual period in which the observed returns are measured.
For example, for returns measured in 2009, companies ranked by size measured by a five-year average net income are placed in portfolios based on their five-year average net income for the period of 2004—2008. This procedure means that there is no hindsight built into the formation of the size ranked portfolios.
Thus, investors choosing to apply size premia from the Risk Premium Report could select companies to include in their portfolios using the same selection criteria as is used in building the portfolios as are reported in the Risk Premium Report each year.
Returns Used in the Risk Premium Report—Size Study Are Not Realistic
Some critics claim that the average returns reported in the Risk Premium Report—Size Study differ from those of some funds targeted at investing in small-cap companies and therefore are unrealistic estimates of expected returns.
In estimating the expected return from an investment in the stock market, one can summarize historic returns by calculating a geometric average return or an arithmetic average return. The arithmetic average of prior period returns is always greater than the geometric average of returns during the same period because it captures the volatility of the realized returns. Both are correct summaries of observed return data.
In cases where an analyst is estimating the expected accumulated wealth at a point in the future, the preferred estimate of the rate of return on an investment in the stock market is the geometric mean of prior period returns or the implied forward return since it includes compounding of returns. But if the analyst is estimating the discount rate that should be used in discounting expected cash flows in future years, the preferred statistic is the arithmetic average of realized returns (realized risk premiums) or the arithmetic average equivalent of implied future returns.[11]
The Risk Premium Report reports the arithmetic average of prior period returns because the data is intended to be used in developing discount rates to be used in discounting expected cash flows in future years.
One commentator compared the arithmetic average returns reported in the Risk Premium Report for 1963 through 2012 to the geometric average returns reported for a fund (DFSCX), which invests in small-cap stocks for the period 1981 through 2015. Any analyst will recognize that this this is a flawed comparison.
The more proper comparison would be to compare the arithmetic average return on the DFA microcap fund for the period 1963 through 2012 with the returns reported in the Risk Premium Report for the same period.
First, to obtain the returns for the period 1963 through 2012, we analyzed the “Ibbotson Associates SBBI U.S. Small Stock TR USD” index, which is constructed as follows:[12]
- DFA U.S. Micro Cap Portfolio (April 2001 to December 2016), the small-cap stock return series is the total return achieved by the net of fees and expenses. At year-end 2016, the DFA U.S. Micro Cap Portfolio contained 1,546 stocks, with a weighted average market cap of $1.128 billion.
- DFA U.S. 9–10 Small Company Portfolio (January 1982 to March 2001; renamed the DFA U.S. Micro Cap Portfolio in April 2001). The fund’s target buy range was a market-cap-weighted universe of the ninth and 10th deciles of the NYSE, plus stocks listed on the NYSE Amex (now the NYSE MKT) and NASDAQ National Market.
- The equities of smaller companies from 1926 to 1980 are represented by the historical series developed by Banz original size premium study.
We can more properly compare the returns for the Ibbotson Associates SBBI U.S. Small Stock TR USD index (essentially the DFA fund used in the commentator’s critique) to the returns reported in the Risk Premium Report.
Second, we can compare the size of the companies included in each. The average market capitalization reported in Appendix A-1 for portfolio 25 in the 2013 Risk Premium Report is $94 million.
At year-end 2012 (the data-through date of the 2013 Risk Premium Report is December 31, 2012), the DFA U.S. Micro Cap Portfolio contained 1,957 stocks, with a weighted average market capitalization of $682 million[13] (the data-through date of the 2013 SBBI “Classic” Yearbook is also December 31, 2012).
The size of companies reported for the DFA U.S. Micro Cap Portfolio should therefore be more properly compared with portfolio 21 where the average market capitalization reported in Appendix A-1 for portfolio 21 in the 2013 Risk Premium Report is $811 million.
The average annual arithmetic return reported in Appendix A-1 for portfolio 21 in the 2013 Risk Premium Report is 16.78%.
The average market capitalization reported Appendix A-1 for portfolio 22 in the 2013 Risk Premium Report is $615 million. The average annual arithmetic return reported in Appendix A-1 for portfolio 22 in the 2013 Risk Premium Report is 17.21%.
The average annual returns reported for the Risk Premium Report portfolios (21 and 22; 16.78% and 17.21%, respectively) that have similar average market capitalizations ($811 million and $615 million, respectively) as the DFA average market capitalization as of December 31, 2012 ($682 million) are similar (the DFA series’ arithmetic average annual return 1963–2012 is 16.2%).
The small differences in returns (16.2% versus 16.78% and 17.21%) may be attributed to many factors (e.g., the Risk Premium Report portfolio returns are equally weighted, so the smaller companies’ intra-portfolios are given equal weight to the larger companies’ intra-portfolios; this weighting will tend to make the Risk Premium Report portfolios have greater returns, all other things held the same, compared to the market weighted returns reported for the DFA fund).
Small Company Stocks Do Not Always Outperform Large Company Stocks
Small companies are believed to typically have greater expected rates of return compared to large companies because small companies are inherently riskier. However, this leaves the question of why small-stock returns have not consistently outperformed large-company stocks for various periods. When talking about expectations, two factors are considered the probability and the magnitude. If small stocks were to always outperform large stocks, this implies that the probability is 100%, which cannot be true. In a recent study, F-F find that the estimated probabilities that small-cap companies can be expected to underperform large-cap companies over a five-year investment horizon is only 29.8%.[14] But they also find that as the investment horizon increases, the likelihood that the returns on small-cap companies will exceed returns of large-cap companies increases:
In short, value and small stock premiums over Market are always risky, but for longer return horizons, good outcomes become more likely and more extreme than bad outcomes.
One can argue that advocates of the size effect can find satisfaction in the erratic performance of small-cap stocks. If you believe that small-company stocks are riskier than large-company stocks, then it probably follows that small-company stocks should not always outperform large-company stocks in all periods. This is true even though the expected returns are greater for small-cap stocks over the long-term.
By analogy, bond returns occasionally outperform stock returns. For example, in 2007, 2008, 2011, and 2014, long-term U.S. government bonds significantly outperformed large-cap company stocks (total return on bonds equaled 9.9% compared to the return on large cap stocks of 5.5% in 2007; 25.9% compared to -37.0% in 2008; 27.1% compared to 2.1% in 2011, and 24.7% compared to 13.7% in 2014), yet few would contend that over longer horizons the expected return on bonds is greater than the expected return on stocks (for the entire period 2007 through 2016, the total returns on long-term U.S. government bonds was less than the returns on large-cap stocks, 6.5% compared to 6.9%).[15]
Richard Bernstein, a well-known market observer wrote:
An important question that is not answered by the doubters of the small stock effect is why smaller capitalization stocks have had performance cycles at all.[16]
We observe that the size effect is cyclical. Readers of the SBBI Yearbooks have long been aware that the small-stock premium (returns of small-cap companies versus large-cap companies) tends to move in cycles, with periods of negative premia followed by periods of high premia. It has been suggested that periods in which small-cap firms have outperformed large-cap firms have generally coincided with periods of economic growth. At least one study contends that the variability in the size effect over time is predictable because large-cap firms generally outperform small-cap firms in adverse economic conditions. Credit conditions are exceedingly important for all firms, but especially for small firms. Small firms generally are at a disadvantage when it comes to financing, and suppliers of debt capital are less likely to lend to small firms in periods of adverse economic conditions.[17] Further, since the late 1990s, many companies have faced a perceived lack of pricing power. In this type of environment, small firms are likely to be at a disadvantage.[18]
For these reasons, analysts should not be surprised to find small-cap stocks underperforming large-cap stocks for lengthy periods of time. The cyclicality is part of the risk of small companies; if small companies always earned more than large companies, small companies would not be riskier in the aggregate.
Size Effect is Inconsistent with the Theory of CAPM
Some argue that the size effect lacks a theoretical basis. First, researchers of the size effect never have claimed that the size effect is anything more than empirical evidence that the CAPM beta does not capture all systematic risk. Critics of the size effect by implication hold that the CAPM beta is the only systematic risk premium. But research has shown that realized returns are not consistent with the returns predicted by the textbook CAPM and its sole risk measure, beta.
F-F published two studies critical of beta. In one study they stated:
The efficiency of the market portfolio implies that (a) expected returns on securities are a positive linear function of their market betas (the slope in the regression of a security’s return on the market’s return), and (b) market betas suffice to describe the cross-section of expected returns.
In that study, F-F observed that the relationship between market beta and average return is flat.[19] In a follow-on study, F-F found that problems with CAPM using U.S. data show up in the same way in the stock returns of non-U.S. major markets.[20]
As authors of one book put it:
Fama and French significantly damaged the credibility of the CAPM and beta.[21]
CAPM stipulates that expected return on an asset is linearly related only to its beta. The model underpins the status of academic finance, as well as the belief that asset pricing is an appropriate subject for economic study. But CAPM has failed the test of reality. Dempsey reexamined the research of Black et al., which did much to lay the empirical foundation for the CAPM. He found that the data do not actually provide a justification of the CAPM as claimed.[22]
Dempsey also criticizes the CAPM foundation that markets are fundamentally rational; empirical evidence casts doubt on the Efficient Market Hypothesis (EMH) and Rational Expectations Hypothesis (REH).
EMH holds that financial prices reflect all available information relevant to the values of the underlying assets—price of an asset converges on its value quickly. The finance industry interpreted EMH to imply market is capable of pricing financial assets correctly and that deviations from fundamental values could not persist.
However, the disappearance of buyers during the Financial Crisis was a severe blow to EMH and Professor Fama, who introduced the EMH, which indirectly criticizes EMH by declaring CAPM is dead.
The REH precludes heterogeneity of expectations is disputed in the literature.
The author concludes that CAPM, EMH, and REH are all about “incredible” assumptions.
When researchers test the CAPM’s cost of equity estimates, they find that realized returns for high-beta stocks are too high (relative to returns predicted by CAPM), and they find that realized returns for low-beta stocks are too low (relative to returns predicted by CAPM). The implications of this work are that if CAPM betas do not suffice to explain expected returns, the market portfolio is not efficient. If this implication is true, then CAPM has potentially fatal problems.
… we argue that the CAPM fails as a paradigm for asset pricing. … a reexamination of the research of Black et al.,[23] which did much to lay the empirical foundation for the CAPM, reveals that the data do not actually provide a justification of the CAPM as claimed, but rather, constitute confirmation of the null hypothesis, namely that investors impose a single expectation of return on assets. Researchers, however, did not wish to abandon the core paradigm of market rationality. Such paradigm, after all, justified the status of finance as a subject worthy of “scientific inquiry.”[24]
More problematic, researchers have shown that stock returns are not normally distributed—a finding that in and of itself demonstrates that beta cannot be the sole measure of risk.[25] The studies have found that distributions of stock returns are skewed[26] and have fatter tails than a normal distribution. Many critics of CAPM hold that the finding of non-normality of returns alone invalidates CAPM. A reasonable likelihood function explaining the distribution of returns as time goes to infinity is the Cauchy distribution; it is a better model of reality than either the normal or the log-normal distribution. But among the characteristics of the Cauchy distribution is that it has no mean; consequently, the central limit theorem does not hold, which negates mean-variance finance as we know it (i.e., negates CAPM, Arbitrage Pricing Theory (APT), and the Black-Scholes Option Pricing Model).
F-F believe that the results of their papers point to the need for pricing risk using a model that is not dependent on beta alone, because beta as traditionally measured is not a complete description of an asset’s risk (or, to put it differently, does not fully explain a security’s realized returns).[27] F-F introduced first a three-factor model and, later, a five-factor model intended to explain stock prices. Both models are empirical in nature and not built upon an underlying theory, and clearly not built upon the textbook CAPM.
The state of our understanding of how asset risk is priced is summed up by Professor John Cochrane:
Discount rates vary a lot more than we thought. The puzzles and anomalies that we face amount to discount rate variation we don’t understand. Our theoretical controversies are about how discount rates are formed … Theories are in their infancy…[28]
Those practitioners that include size premia in their estimates of the cost of equity when applying the MCAPM are simply applying an empirically observed correction to the incomplete or defective textbook CAPM. Why should practitioners be faulted for correcting an incomplete or a defective model?
There continues to be critiques of the size effect in the academic literature, most often focused on the difficulty of using the size effect in building portfolios and effectively implementing a profitable trading strategy, not focused on estimating the cost of capital.[29]
This article was previously published in the American Society of Appraisers’ Business Valuation Review, Vol 37(3) Fall 2018, and is re-published here with permission.
Roger J. Grabowski, FASA, is a managing director with Duff & Phelps and an Accredited Senior Appraiser and Fellow (FASA) of the American Society of Appraisers (ASA) (their highest designation).
He was formerly Managing Director of the Standard & Poor’s Corporate Value Consulting practice, a partner of PricewaterhouseCoopers LLP and one of its predecessor firms, Price Waterhouse (where he founded its U.S. Valuation Services practice and managed the real estate appraisal practice).
He has directed valuations of businesses, interests in businesses, intellectual property, intangible assets, real property and machinery and equipment. Mr. Grabowski has testified in court as an expert witness on matters of solvency, the value of closely held businesses and business interests, valuation and amortization of intangible assets and other valuation issues. His testimony in U.S. District Court was referenced in the U.S. Supreme Court opinion decided in his client’s favor in the landmark Newark Morning Ledger case.
Mr. Grabowski is co-author with Shannon Pratt of Cost of Capital: Applications and Examples, fifth edition. (John Wiley & Sons, 2014), The Lawyer’s Guide to Cost of Capital (ABA, 2014), and Cost of Capital in Litigation: Applications and Examples (John Wiley & Sons, 2010). He is a contributor to the Duff & Phelps on-line Cost of Capital Navigator platform and he is co-author of the Duff & Phelps annual books: Valuation Handbook-U.S. Industry Cost of Capital, Valuation Handbook—International Guide to Cost of Capital and Valuation Handbook—International Industry Cost of Capital.
Mr. Grabowski teaches courses for the American Society of Appraisers and is a frequent guest lecturer at NACVA Annual Conferences.
Mr. Grabowski can be contacted at (312) 697-4720 or by e-mail to Roger.Grabowski@duffandphelps.com.
[1] https://quickreadbuzz.com/2017/02/15/shouldnt-add-size-premium-capm-cost-equity/
[2] Kent Daniel, Mark Grinblatt, Sheridan Titman, and Russ Wermers, “Measuring Mutual Fund Performance with Characteristic‐Based Benchmarks,” The Journal of Finance 52(3) (1997): 1035–1058.
[3] Clifford S. Asness, Andrea Frazzini, Ronen Israel, Tobias J. Moskowitz, and Lasse Heje Pedersen, “Size Matters, If You Control Your Junk,” Journal of Financial Economics 129 (2018): 479–509.
[4] Statman, Meir. “How many stocks make a diversified portfolio?” Journal of Financial and Quantitative Analysis 22, no. 3 (1987): 353–363.
[5] Ravi Jagannathan and Zhenyu Wang. “The Conditional CAPM and the Cross‐Section of Expected Returns.” The Journal of Finance 51(1) (1996): 3–53.
[6] Gordon J. Alexander and Norman L. Chervany, “On the Estimation and Stability of Beta,” Journal of Financial and Quantitative Analysis 15 (01) (March 1980): 123–137; Gabriel Hawawini, “Why Beta Shifts as Return Interval Changes,” Financial Analysts Journal (May/June 1983): 73–77; Tolga Cenesizoglu, Qlanoiu Liu, Jonathan J. Reeves and Haifeng Wu, “Monthly Beta Forecasting with Low-, Medium- and High-Frequency Stock Returns,” Journal of Forecasting (2016) wileyonlinelibrary.com DOI: 10.1002/for.2396.
[7] Published in 2014 through 2017 in the annual Duff & Phelps Valuation Handbook—U.S. Guide to Cost of Capital and now available through the online Cost of Capital Navigator online platform at dpcostofcapital.com.
[8] There is still an ongoing debate about what is the SP. According to Fama and French (Eugene F. Fama and Kenneth R. French, “The Cross‐Section of Expected Stock Returns.” The Journal of Finance 47(2) (1992): 427–465; “Common Risk Factors in the Returns on Stocks and Bonds. “Journal of Financial Economics 33(1) (1993): 3–56; “Multifactor Explanations of Asset Pricing Anomalies.” The Journal of Finance 51(1) (1996): 55–84), it is a risk premium. According to Kent Daniel, Mark Grinblatt, Sheridan Titman, and Russ Wermers (“Measuring Mutual Fund Performance with Characteristic-Based Benchmarks,” The Journal of Finance 52(3) (1997)” 1035–1058), it is not a compensation for risk. This discussion is beyond the scope of this paper.
9 The author cites Yahoo finance website as a reference for the use of a three-year look-back period. Most finance text books recommend the use of five years as a rule of thumb for the look-back period.
[10] Access at http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html accessed August 8, 2018.
[11] “Using the Geometric Average for Compounding and the Arithmetic Average for Discounting,” in Cost of Capital: Applications and Examples 5th ed. (Hoboken, New Jersey: John Wiley & Sons, Inc., 2014), 153–159.
[12] 2017 SBBI Yearbook, Chapter 3, “Description of the Basic Series” pages 3.2 and 3.3.
[13] 2013 SBBI “Classic” Yearbook, Chapter 3 “Description of the Basic Series,” page 54.
[14] Eugene F. Fama and Kenneth R. French, “Volatility Lessons,” Financial Analysts Journal 74(3) (2018) 42–53.
[15] 2017 SBBI Yearbook.
[16] Richard Bernstein, Style Investing: Unique Insights into Equity Management (New York: John Wiley & Sons, 1995): 142.
[17] Ching-Chih Lu, “The Size Premium in the Long Run,” Working paper, December 2009. The author reports on a study he conducted comparing the average market values of common equity between companies with investment-grade credit ratings and those with non-investment-grade credit ratings for the period 1994–2008. He found that the companies with better credit ratings were nine to ten times larger than the companies with poorer credit ratings.
[18] Satya Dev Pradhuman, Small-Cap Dynamics: Insights, Analysis, and Models (New York: Bloomberg Press, 2000): 23–28.
[19] Eugene Fama and Kenneth French, “The Cross-Section of Expected Stock Returns,” Journal of Finance 57(2) (June 1992): 427–465.
[20] Eugene Fama and Kenneth French, “Value versus Growth: The International Evidence,” Journal of Finance (December 1998): 427–465.
[21] Tim Koller, Marc Goedhart, and David Wessels, Valuation—Measuring and Managing the Value of Companies, 5th ed. (Hoboken, NJ: John Wiley & Sons, 2010): 256.
[22] Mike Dempsey, “The Capital Asset Pricing Model (CAPM): The History of a Failed Revolutionary Idea in Finance?” Abacus 49, Supplement (2013): 7.
[23] Michael C. Jensen, Fischer Black, and Myron Scholes, “The Capital Asset Pricing Model: Some Empirical Tests,” in M. Jensen (ed.), Studies in the Theory of Capital Markets (New York: Praeger Publishers, 1972).
[24] Mike Dempsey, “The Capital Asset Pricing Model (CAPM)” The History of a Failed Revolutionary Idea in Finance?” Abacus 49, Supplement (2013):8.
[25] Hsing Fang and Tsong-Yue Lai in “Co-kurtosis and Capital Asset Pricing,” Financial Review (May 1997): 293–307, derive a four-moment CAPM and show that systematic variance, systematic skewness, and systematic kurtosis contribute to the risk premium, not just beta; Fred Arditti in “Risk and the Required Return on Equity,” Journal of Finance (March 1967): 19–36, demonstrates that skewness and kurtosis cannot be diversified away by increasing the size of the portfolios.
[26] Skewness describes asymmetry from the normal distribution in a set of statistical data. Skewness can come in the form of negative skewness or positive skewness, depending on whether data points are skewed to the left (negative skew) or to the right (positive skew) of the data average.
[27] Eugene Fama and Kenneth French, “The Cross-Section of Expected Stock Returns,” The Journal of Finance 47(2) (1992):427–465.
[28] John C. Cochrane, University of Chicago Booth School of Business, “Presidential Address: Discount Rates,” Journal of Finance” 66(4) (2011): 1047–1108.
[29] For example, see Ron Alquist, Ronen Israel and Tobias Moskowitz, “Fact, Fiction, and the Size Effect,” Journal of Portfolio Management (forthcoming) https://ssrn.com/abstract=3177539. Many of these criticisms are addressed in Chapter 15, “Criticisms of the Size Effect,” Cost of Capital: Applications and Examples 5th ed. (Hoboken, New Jersey; John Wiley & Sons, Inc., 2014).

