Estimating Debt Betas and Beta Unlevering Formulas

Use of Benninga-Sarig to Estimate Debt Betas in a Valuation Engagement

In the July 8, 2016 In re Appraisal of DFC Global Corp. Opinion (DFC Opinion), the Court of Chancery of the State of Delaware suggested that debt betas should be estimated for individual companies and it cited Pratt and Grabowski’s Cost of Capital as a source for debt betas based on the firm’s credit rating. In addition, the Court also adopted the Hamada Formula over the Fernandez Formula to unlever betas because it believed the Hamada Formula “is widely accepted, readily understood, and not subject to dispute about whether it is properly calculated.” In this article, Clifford Ang critiques these two approaches and argues these two approaches may not be the best practice for valuation practitioners.

[su_pullquote align=”right”]Resources:

The Great Debate over Total Beta, Part 1

The Great Debate over Total Beta, Part 2

Emerging Issues in Cost of Capital: A Deep Dive Into the D&P Handbook and Beyond

2017 Duff & Phelps Valuation Handbook—Guide to Cost of Capital

[/su_pullquote]

In the July 8, 2016 In re Appraisal of DFC Global Corp. Opinion (DFC Opinion), the Court of Chancery of the State of Delaware suggested that debt betas should be estimated for individual companies and it cited Pratt and Grabowski’s Cost of Capital as a source for debt betas based on the firm’s credit rating.[1]  In addition, the Court also adopted the Hamada Formula over the Fernandez Formula to unlever betas because it believed the Hamada Formula “is widely accepted, readily understood, and not subject to dispute about whether it is properly calculated.”[2]  As I explain below, using these two approaches may not be the best practice for valuation practitioners.

Estimating Debt Betas

Practical issues make estimating debt betas directly from the firm’s bonds extremely challenging, if not impossible.  Specifically, firms may issue many bonds and the heterogeneity of those bonds may make identification of a representative bond difficult.  In addition, even if such a bond could be identified, the bond markets are very illiquid and finding a reliable price series for such a bond could prove challenging.  As an alternative, the Court in the DFC Opinion suggested using debt betas by credit rating reported in Pratt and Grabowski’s Cost of Capital.  

In that book, the authors estimate debt betas using the Benninga-Sarig “tax adjusted cost of debt SML [Security Market Line],” which is     

where R_D is the cost of debt, R_F is the risk-free rate, β_D is the debt beta, R_M is the return on the market, and t is the corporate tax rate.  The Benninga-Sarig formula was developed to arrive at a CAPM-like approach when there are different tax rates for debt and equity and this methodology, in addition to modifying the SML for debt, also requires a modified equity SML equation (i.e., you are no longer using the CAPM) and a modified beta unlevering formula (i.e., you cannot use the standard beta unlevering formulas, such as those discussed below).[3]  As a consequence, the debt betas reported in Cost of Capital are calculated in a manner that is inconsistent with the CAPM that is used by practitioners.

Moreover, in a later edition of the financial modeling book relied upon in the Cost of Capital, even the author questions the usefulness of the formula he developed.  Specifically, Benninga writes:

“Although the tax-adjusted CAPM is more consistent with an economy with taxation, we confess that—given the uncertainties surrounding cost of capital computations—the difference between the classic CAPM and the tax-adjusted CAPM may not be worth the trouble.”[4]

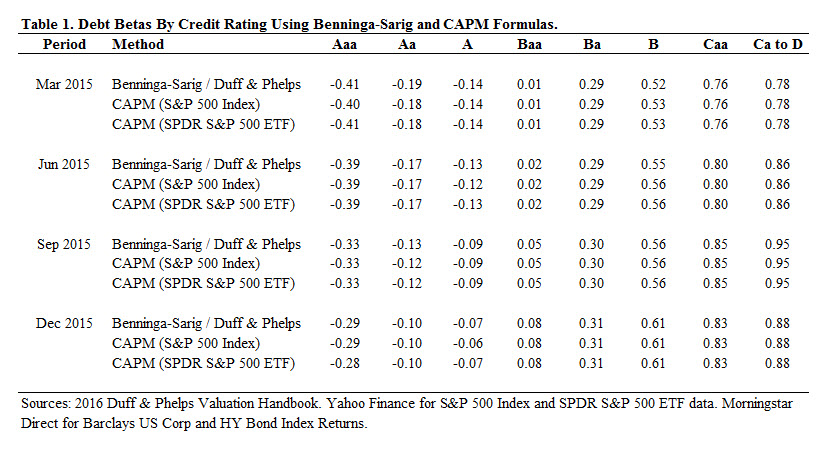
Therefore, we have to determine whether there are any benefits to using the Benninga-Sarig formula.  As a simple test, I compare the debt betas reported in the Duff & Phelps 2016 Valuation Handbook, which uses the same Benninga-Sarig formula as the Cost of Capital but using updated data for the four quarters of 2015 against debt betas calculated using the CAPM.[5]  For robustness, I use two market proxies for my market model: S&P 500 Index and the SPDR S&P 500 ETF.  I obtain price data for the two market proxies from Yahoo Finance.  Following the methodology in the Duff & Phelps Valuation Handbook, I use the Barclays U.S. Corp and HY Bond Indexes from Morningstar Direct for the bond index data by credit rating and the debt betas are estimated using five years of monthly returns.  The results of my test are reported in Table 1.

As Table 1 shows, there is virtually no difference in the calculated betas using the Benninga-Sarig formula and the CAPM.  Therefore, there appears to be no practical benefit to using the Benninga-Sarig debt betas over the CAPM that would offset the need to deviate from the CAPM and standard beta unlevering formulas.  Moreover, using the CAPM gives the added benefit of allowing the valuation practitioner to use a consistent methodology to calculate both the equity and debt betas (i.e., using the same return interval and estimation period).

Fernandez vs. Hamada Unlevering Beta Formulas

The Court in the DFC Opinion favored the use of the Hamada Formula to unlever debt betas over the Fernandez Formula because it opined that the Hamada Formula “is widely accepted, readily understood, and not subject to dispute about whether it is properly calculated.”[6]  This observation is interesting because only one input differentiates the two formulas.  To see how, note that the Fernandez formula is

where β_L is the levered beta, β_U is the unlevered beta, β_D is the debt beta, t is the corporate tax rate, D is the value of debt, and E is the value of equity.[7]  If we assume that β_D = 0, then Eq. (1) becomes

which is the Hamada Formula.  Therefore, the important question when choosing between these two formulas boils down to how reasonable is an assumption that the firm’s debt beta is equal to zero.

For at least three reasons, I argue it is highly unlikely that a firm’s debt would have a beta of zero, which supports the use of an unlevering formula that incorporates a non-zero debt beta such as the Fernandez Formula.  First, based on the CAPM, a zero-beta asset is expected to yield the risk-free rate of return, but investors will likely not consider investing in many, or any, corporate debt if the debt were only expected to yield the risk-free rate.  Second, prior studies report debt betas for broad ratings categories that are not equal to zero.  For example, in 1991, Cornell and Green published a paper that reported high-grade bonds have a debt beta of 0.25 and low-grade bonds have a debt beta of 0.29[8] and, in 2011, Groh and Gottschalg published a paper that reported high-grade bonds have a beta of 0.296 and low-grade bonds have a beta of 0.410.[9]  Third, as shown in Table 1, debt betas regardless of credit ratings are unlikely to equal zero.

Summary

In the DFC Opinion, the Court implicitly suggested the use of two procedures: the Benninga-Sarig formula to estimate debt betas and the Hamada formula to unlever betas.  As shown above, debt betas estimated using the Benninga-Sarig formula require the use of a different Security Market Line and beta unlevering formula, but the ultimate results are virtually identical to debt betas estimated using the CAPM.  We also showed that the Hamada formula is the Fernandez formula when you assume a debt beta of zero, but the zero debt beta assumption required by the Hamada formula unlikely holds in practice.  Therefore, using these two approaches may not be the best practice for valuation practitioners.

* Vice President at Compass Lexecon. E-mail: cang@compasslexecon.com. Opinions expressed herein are solely those of the author and are not opinions of Compass Lexecon or its other employees.

[1] DFC Opinion note 144.

[2] DFC Opinion at 33.

[3] Benninga, S. and O. Sarig. 2003. “Risk, Returns, and Values in the Presence of Differential Taxation.” Journal of Banking & Finance 27, pp. 1123–1138.

[4] Benninga, S. 2014. Financial Modeling, 4^th ed. MIT Press, p. 98.

[5] Consistent with what is typically done in practice, I estimate betas using a market model of the form: R_D = a + b * R­_M.

[6] DFC Opinion at 33.

[7] This formula appeared in a published article in 2004 by Fernandez [“The Value of Tax Shields Is Not Equal to the Present Value of Tax Shields,” Journal of Financial Economics 73, p. 145–165]. However, the form of the Fernandez Formula has been derived from beta factors based on the CAPM in a published article in 1982 by Yagill [“On Valuation, Beta, and the Cost of Equity Capital: A Note,” The Journal of Financial and Quantitative Analysis 17, pp. 441–449].

[8] Cornell, B. and K. Green. 1991. “The Investment Performance of Low-Grade Bond Funds.” The Journal of Finance 46, pp. 29–48, at p. 34.

[9] Groh, A. and O. Gottschalg. 2011. “The Effect of Leverage On the Cost of Capital of U.S. Buyouts.” Journal of Banking & Finance 35, pp. 2099–2110, at p. 2019.

Clifford S. Ang, CFA is Vice President at Compass Lexecon, an economic consulting firm that specializes in the application of economics to a variety of legal and regulatory issues. He works out of the Chicago, IL and Oakland, CA offices. Mr. Ang specializes in the areas of valuation, corporate finance, accounting, and damages. He has worked on hundreds of engagements involving companies across a broad-spectrum of industries concerning issues such as valuation, solvency, market efficiency, materiality, loss causation, and damages. Mr. Ang is also the author of Analyzing Financial Data and Implementing Financial Models Using R.
Mr. Ang can be reached at (510) 285-1285 or by e-mail to cang@compasslexecon.com.