The Objective Case for a Key Person Discount
Apply the Key Person Discount
Is there any evidence that a key person discount exists? In this article, Steven Egna, shares his views on the subject matter and provides an illustration of the statistical basis for supporting such a discount.
[su_pullquote align=”right”]Resources:
Relevance, Reliability, and the Company-Specific Risk Premium
EBITDA Single Period Income Capitalization for Business Valuation
Advanced Discounts and Premiums
Intermediate Business Valuation Certification and Training Center
[/su_pullquote]
I was recently consulted on the valuation of a lobbying business that relied heavily upon the experience of the owner. Fair market value was the standard and the whole business was being valued. The market data for lobbying firms is nearly non-existent and since there were virtually no tangible assets to speak of, an Asset-based Approach was clearly not an option. This left the Income-based Approaches as the only viable avenues to follow.  The major concern with the Income Approach was that consideration of only the systematic risk of a lobbying business would not adequately reflect the difficulty in transferring a business of this nature.  Three options came to mind to address this situation. One would be to apply a company specific risk premium in the determination of the discount rate. Another would be to apply a discount for lack of marketability, as the number of buyers with the expertise and political connections to assume the role of the current owner would be very limited. The other possible approach would be to apply a key person discount.
Without reliable market data, a subjective adjustment under the Income Approach would need to be applied, in the form of company specific risk, discount for lack of marketability, or a key person discount. However, before assessing the magnitude of the subjective adjustment, in whatever form, it struck me that I needed some objective basis for even asserting that a discount, in some form or another, was reasonable and appropriate. How can an appraiser (or anyone for that matter) show, objectively, that the value of a professional services business heavily reliant upon the experience of its owner would be less valuable than a business without such a reliance?
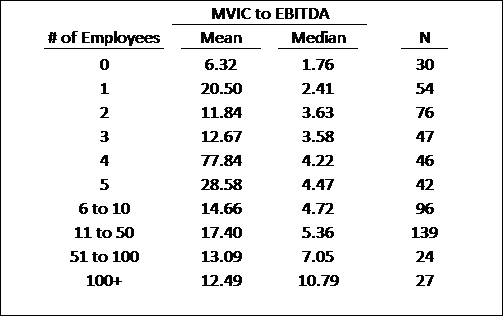
My solution was to consider the valuation multiples observable in the sale of professional, scientific, and technical service businesses. Data was extracted for the sale of all businesses under the NAICS code 541 using the Pratt’s Stats database. The data included sold firms across a broad range of industries, from aviation services to web design, with nearly 2,000 transactions found, 581 transactions had the necessary data for the analysis. Next, the transactions were sorted by the number of employees at the sold firm and the observed median Market Value of Invested Capital-to-EBITDA multiple (MVIC-to-EBITDA). The results are shown in the table below.  My hypothesis was that firms with fewer employees would sell for lower multiples, on the basis that the relationships with customers were more dependent on one or a few key persons at smaller firms than at larger firms.
As shown, the mean MVIC to EBITDA multiples observed do not appear to support my hypothesis of smaller multiples for smaller firms. After going through the details of the transactions a bit more, it appeared that the relatively high mean multiples are a function of the occasional transaction with a purchase price equal to 30 times EBITDA or more. While it is tempting to call these outliers, and strike them from the dataset, there are, in my opinion, too many of these high-multiple transactions, 56 (almost 10% of the dataset used), to call them outliers. Furthermore, because the MVIC-to-EBITDA multiples were not normally distributed and the sample size, especially for the zero-employee category, is not large, a standard t-test of means is not appropriate.[1] However, for non-normally distributed data with small sample sizes, there is an alternative, non-parametric test[2], known as the Wilcoxon Rank Sum Test (WRST). The WRST does not require normally distributed data and works on small sample sizes.
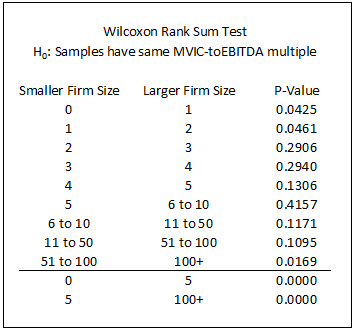
A full explanation of the WRST is beyond the scope of this article; in brief, the WRST takes two samples (e.g., the EBITDA multiples from the companies with no employees and the EBITDA multiples from the companies with one employee), merges them, ranks them from highest to lowest, and then sums the rankings of each sample. Next, the sums of the rankings are compared. If the two samples were taken from populations with similar centers of their respective distributions, then we would expect their rank sums to be approximately equal. If the rank sums are sufficiently different, we can conclude that the centers of their distributions are not the same. Statistical software (in this case the open source software GRETL was used) indicates the likelihood that the distributions are the same with a measure known as a “p-value.”[3] The lower the p-value, the less likely that the centers of the distribution are the same.  The table below shows the p-values for comparisons of the median MVIC-to-EBITDA multiples based on the number of employees. A p-value below .05 indicates that the likelihood of observing such an outcome by random chance is less than five percent, leading to the conclusion that the firms with fewer employees sell at lower multiples.
As the results from the WRST show, we can be confident in the assertion that valuation multiples increase with the number of employees. This is true as we go from firms with no employees to firms with just one employee. Statistically, the employee size-EBITDA multiple relationship is not so precise that we can observe it incrementally for every employee added. So, we see no statistical difference in the EBITDA multiple as we go from, say, two to three or three to four employees. However, it appears that the relationship is strong enough that when we make comparisons of the multiples for firms with no employees to those for firms with five employees or larger, we get p-values telling us that there is less than a one in 100,000 chance that the firms with no employees sell for an EBITDA multiple that is equal to or greater than that of the firms with five employees. Similarly, there is less than a one in 40,000 chance that firms with five employees sell for multiples greater than or equal to that of firms with more than 100 employees.
The analysis above provided me with the foundation to discount the value of the lobbying business based on the importance of the key person/owner. Although the approach for implementing the discount and subjectively assess its magnitude had to be determined, an objective basis for the existence of the discount had been established.
[1] Comparing means using a t-test is appropriate when there is a large sample size or, with a small sample size if the population from which the sample is drawn is normally distributed.
[2] Non-parametric means that the test works independent of the distribution of the underlying data.
[3] A p-value measures the area of the distribution that exceeds the value of the test statistic. It reflects the probability that the tested statistic could take on the observed value even though the null hypothesis (i.e., opposite what is being tested for) is correct. Applied here, it means that we would observe the differences in the median multiples with a probability of “p-value” even if the median multiples were actually equal.
Mr. Egna is one of the leaders of the Valuation Resource Group, an East Greenbush, New York, M&A, advisory, transition planning, valuation, and pension appraisal professional services firm. Mr. Egna has over 30 years of diversified financial leadership and management experience specializing in transition planning and valuation analysis of all sorts. He brings a practical, hands-on approach to all of his work. Steven M. Egna is a Certified Business Appraiser™ (CBA™) accredited by the Institute of Business Appraisers™; a Certified Valuation Analyst® (CVA®) and Accredited in Business Appraisal Review™ (ABAR™) accredited by the National Association of Certified Valuators and Analysts®; he is also a Certified Merger and Acquisition Advisor (CM&AA®) accredited by the Alliance of Merger & Acquisition Advisors®.
Mr. Egna can be reached at: (518) 479-1008 or by e-mail to: SEgna@valuationresource.com.