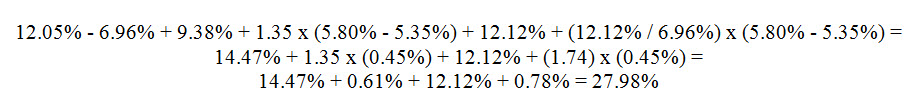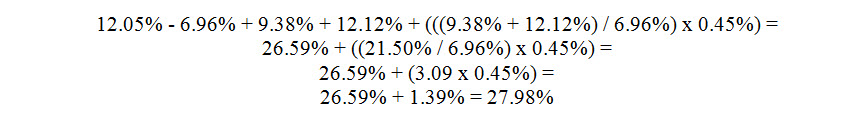Modified Formula for Adjusting Cost of Capital
For Current Market Conditions
How can one adjust the cost of capital to reflect current market conditions? Does inclusion of the βSIZE and SPH/ERPH result in double counting? In this article, Marc Vianello answers these questions.
 I made a recent presentation called “Cost of Capital for Prevailing Market Conditions” at the NACVA Business Valuation Conference in Pittsburg, PA. This presentation demonstrated my concept for using a stock index such as the S&P 500 and the corresponding earnings per share of the index to calculate a market capitalization rate as of a particular date, which can then be used with cost of capital data, such as the Duff & Phelps 2014 Valuation Handbook, to calculate date-specific cost of capital that reflects current market conditions.[1] Slide 27 of my presentation presented a formula to describe the mechanics of calculating a cost of equity capital based on market conditions. The formula was stated as follows:
I made a recent presentation called “Cost of Capital for Prevailing Market Conditions” at the NACVA Business Valuation Conference in Pittsburg, PA. This presentation demonstrated my concept for using a stock index such as the S&P 500 and the corresponding earnings per share of the index to calculate a market capitalization rate as of a particular date, which can then be used with cost of capital data, such as the Duff & Phelps 2014 Valuation Handbook, to calculate date-specific cost of capital that reflects current market conditions.[1] Slide 27 of my presentation presented a formula to describe the mechanics of calculating a cost of equity capital based on market conditions. The formula was stated as follows:
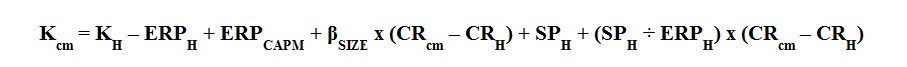
Where:
With the exception of CRcm and CRH, all of the values assumed for the defined terms come from Exhibit 7.3 of the 2014 Valuation Handbook.[2]
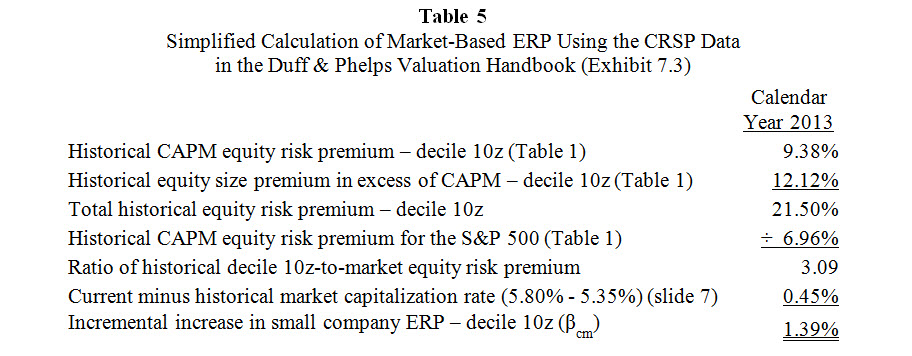
Slide 21 of my presentation showed that a 0.45% change in the market capitalization rate relative to a long-term average market capitalization rate (e.g., from 5.80% versus 5.35%) equates to a 1.39% change in the equity risk premium (ERP) of an Ibbotson decile 10z company using the values shown in Exhibit 7.3 of the 2014 Valuation Handbook. Table 5 below is from slide 21 of my presentation. It uses the information from Exhibit 7.3 to calculate the 1.39% cost of capital adjustment:
An ERP change of 1.39% has the effect of increasing the long-term average cost of equity capital of a decile 10z company from 26.59% to 27.98%, as shown in slide 23 of my presentation. Applying the values shown in the above term definitions to the formula as stated results in the following math:
Note that the components 0.61% + 0.78% above equal 1.39%, which is the expected change in ERP due to current market conditions.
During my presentation, Ashok Abbot, Ph.D., raised an objection to the formula as stated. If I recall his objection correctly, he asserted that the variable βSIZE is the same beta as results from (SPH / ERPH), thereby double counting the beta. But clearly that is not the case since the decile 10z value for βSIZE reported by Duff & Phelps is 1.35 while the calculated value of (SPH / ERPH) is 1.74. The distinction is that βSIZE is the historical CAPM size beta, while (SPH / ERPH) represents the historical size premium in excess of ERP as predicted by CAPM, divided by the historical equity risk premium of the market. The two betas are measuring different things, and there is no double counting.
After my presentation, I concluded that I could restate the above formula in a simpler form that eliminates two of the defined terms that led to Dr. Abbot’s confusion. This restated formula is:
Applying the assumptions stated in the term definitions to the formula results in this math:
Both formulas yield the same mathematical result. And both formulas allow practitioners to craft a cost of capital that is specific to the market conditions extant on the valuation date. One advantage of the restated formula is that it eliminates the confusion that led to Dr. Abbott’s criticism. Another advantage is that the restated formula can be used with both the CRSP data and the Risk Premium Report data included in the 2014 Valuation Handbook.
[1] My presentation was based on an article that I authored called “A Method to Adjust the Cost of Equity Capital for Prevailing Market Conditions” that was published by the AICPA in May 2015 in FVS Consulting Digest.
[2] βSIZE is assumed to be a factor of 1.35. Slide 27 of my presentation erroneously stated the assumption as 1.35%.
Mr. Vianello, CPA, ABV, CFF, is the Managing Member of Vianello Forensic Consulting, LLC. He is the inventor of the concept of probability-based discount for lack of marketability using the Longstaff look-back formula, and is the developer of the VFC DLOM Calculator. He has written extensively regarding DLOM, the time periods needed to sell privately held businesses, the specific company risks associated with abnormal debt levels, and adjusting cost of capital for prevailing market conditions. Mr. Vianello can be reached at (913) 432-1331 or e-mail Vianello@vianello.biz.