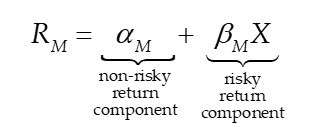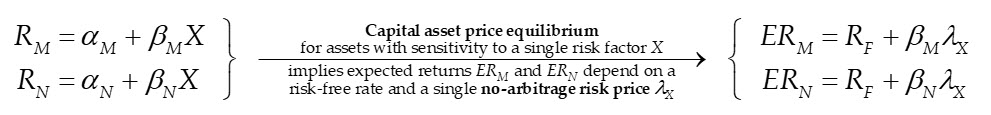Understanding IPCPL Theory, Evidence, and Application

Use in Private-Business Valuation (Part II of II)

This two-part article in this continuing series explains the implied private company pricing line (IPCPL). Read Part I here. IPCPL explains and predicts how buyers and sellers of capital assets in private markets set risk-adjusted discount rates under conditions of non-zero transaction cost differentials between public and private markets; and, accordingly, IPCPL explains and predicts the shadow price of liquidity risk—the price of liquidity risk were it traded directly in private capital markets.

1.4 What is lacking in existing business valuation theory?

It turns out that existing business valuation theory is lacking in two distinct aspects in the context of privately-held and traded capital assets: no-arbitrage risk pricing and private capital market transaction costs. As will be shown, IPCPL applies to the latter.

No-arbitrage risk pricing. It can be seen in Section that there is actually little coherent theory on how buyers and sellers of privately-held capital assets set risk-adjusted discount rates. However, the two-sentence theory summary presented in Section carries with it precisely what is lacking in business valuation theory:

Value today always equals future cash flow discounted at the opportunity cost of capital.

[The market approach] is based on the economic principle of substitution.

(Hitcher, 2017, p. 118 and p. 290, respectively.)

An explanation and prediction of how opportunity cost of capital (OCC) is determined under the economic substitution principle and fair capital market conditions, specifically for privately-held capital assets. To see the issue more clearly, consider the following definitions.

OCC: OCC is the expected return available on the next best investment of equivalent risk (see, e.g., McLelland, 2019, p. 26).

Economic substitution principle: Hitcher (2017, p. 291) notes that the economic substitution principle implies “a rational … buyer will not pay more … than the current price for a comparable company” (but comparable is not defined), while International Valuation Standards indicate all valuation approaches are “based on the economic principles of price equilibrium … or substitution” (2011, p. 12). In a capital market equilibrium, economic substitution results from asset prices being adjusted based on their relative risk exposures and sensitivities.

These two definitions imply something important about private capital asset valuation that has not been made clear in business valuation theory—price equilibrium in capital markets characterized as fair markets implies there are no risk arbitrage opportunities in the markets, i.e., the price of risk in any of such markets is equal across the markets.

To understand this idea, consider the simplest example where the capital market returns of a publicly-traded asset M (R_M) are correlated with only a single risk factor (X); meaning in the following equation, beta (b_M) represents the sensitivity to the risk.

In this simplest example, there is another asset N also with a non-zero sensitivity (b_N) to the single risk factor X, which generally differs from the sensitivity of asset M to the risk. Then rational investors would interact in fair capital markets—i.e., open and competitive capital markets—such that the expected returns to assets M and N depend on the same price of risk X; denoted l_X.

Capital markets trade risks

As suggested by the no-arbitrage risk price result shown immediately above, arbitrage pricing theory implies that what is being priced and traded in capital markets are not assets, per se; fundamentally, it is risks that are being priced and traded.

So, regardless of whether assets M or N are traded in the same market (e.g., U.S. vs. Brazilian markets, or public vs. private capital markets, etc.) as long as both are traded in fair markets, then the no-arbitrage risk price condition must hold. This is precisely the basis—and the only basis—for using public capital market data to estimate the FMV of privately-held capital assets. Moreover, no-arbitrage risk pricing obviates the problem of identifying and using data from so-called comparable companies in valuation analyses. The no-arbitrage risk price l_X represents the expected rate of return from holding one unit of pure risk X and, therefore, when weighted by each asset’s risk sensitivity precisely represents each asset’s risk-adjusted expected rate of return. And it can be shown that this risk-adjusted expected fair market rate of return precisely meets the definition of OCC presented above.

The no-arbitrage risk pricing is critical to understand not only in terms of its general relevance to business valuation theory, but also in its relationship to IPCPL theory. Again, IPCPL theory does not replace existing capital asset pricing theory, it simply augments the theory such that it explains and predicts private capital asset valuations.

Private capital market transaction costs pose two issues with respect to business valuation theory: (i) Observable asset price data in both public and private capital markets might not generally represent FMV as defined in the valuation literature, and (ii) transaction costs differ across capital market settings including between public and private markets. To understand the issues, consider the following expression.

This expression is a tautology defining transaction costs as any net difference between the unobservable FMV and the ex post observable transaction price of the asset. It is helpful to rewrite this for emphasis where transaction costs (TC) and, therefore, transaction price (P) vary depending on the capital market in which the asset trades (m).

The implication is that observable capital market price data used in business valuation does not—in principle—represent FMV; but, rather, FMV after net transaction costs. And this is the case whether the price data is obtained from either public or private capital market transactions. If the objective is to estimate FMV, then theory and methods are needed to estimate net capital market transaction costs, i.e., the difference between observable transaction price and unobservable FMV.

This section has demonstrated two significant aspects of business valuation theory that are lacking in terms of explaining and prediction what buyers and sellers of capital assets do:

(i)   Existing business valuation theory lacks a clear explanation and prediction of how buyers and sellers of privately-held and traded capital assets estimate opportunity cost of capital in terms of no-arbitrage risk pricing.

(ii)  Existing business valuation theory lacks a clear explanation and prediction of how buyers and sellers of capital assets estimate transaction costs for the purpose of estimating the FMV of capital assets.

IPCPL theory explains and predicts how to estimate transaction costs in private capital market transactions. In this connection, it derives implications augmenting existing methods of estimating opportunity cost of capital for privately-held capital assets.

1.5 What does IPCPL theory explain and predict? 

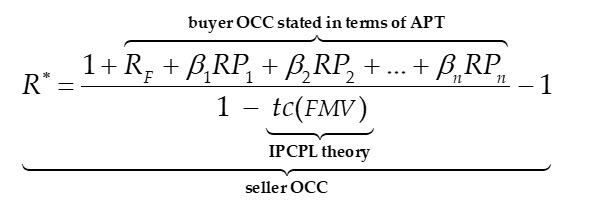
Based on the foregoing discussion, the question of precisely what IPCPL theory explains and predicts can be answered in a clear, concise way. It is best to begin with the simplest expression of the no-arbitrage condition between a capital asset buyer and seller in the presence of transaction costs.

After algebraic rearrangement, the relationship between buyer and seller OCC and the domain of IPCPL theory explanations and predictions.

More explicitly with respect to buyer OCC, seller OCC can be written in terms of an accepted OCC estimation method according to Hitchner (2017); see again Section .

With this expression, it now seems the question of “What is IPCPL Theory?” has now been answered in a basic way, so a more detailed discussion of IPCPL theory will be deferred to the future articles in this series.

1.6 Future issues

In the remaining articles in this series, we will address the following questions with respect to IPCPL theory:

Part 2: How to understand IPCPL theory?

Part 3: What is the evidence supporting IPCPL theory?

Part 4: How can IPCPL be applied in practice?

1.7 Glossary

The economic principle of substitution states that a rational buyer will not pay more for a good or service than the cost of an equally desirable substitute.

The law of one price (LOOP) is an economic principle that states that identical goods or assets should sell for the same price in different markets, after taking into account transaction costs, transportation costs, and currency exchange rates. This law is based on the assumption that arbitrage will eliminate any price discrepancies between markets.

The no-arbitrage principle is a fundamental concept in finance that states that there should be no risk-free opportunities to make a profit. In other words, if there is a way to make a profit without taking any risk, then investors will take advantage of this opportunity until it is no longer profitable. This will cause the prices of assets to adjust until there are no more arbitrage opportunities.

A fair market is an idealized market where buyers and sellers are informed and have equal bargaining power. In this type of market, prices are set by the forces of supply and demand, and there is no coercion or manipulation.

---

David Goodman, MBA, CPA, CVA, has 25 years of experience in performing business valuations and forensic accounting services for family law and business disputes. He also has prepared business valuations for tax and buy-sell purposes. He has an MBA from the Amos Tuck School at Dartmouth College. He is a past-president of the NACVA-Mass State Chapter, past chair of the Massachusetts Society of Certified Public Accountants Litigation and BV committee, and a past board member and treasurer of the Massachusetts Collaborative Law Council. As a financial neutral, Mr. Goodman has helped divorcing couples reach peaceful equitable solutions. He has presented on business valuation and tax issues related to divorce at NACVA annual conference, NACVA-Mass. State Chapter, and the Massachusetts Collaborative Law Council. He has also testified as an expert witness in court and arbitration. He is currently serving on the editorial board of QuickRead.

Mr. Goodman can be contacted at (617) 698-3950 or by e-mail to dgoodman@joacpa.com.

Malcolm McLelland, PhD, has 40 years of professional and academic experience in finance and accounting, including positions in commercial banking, consulting, and educational institutions. His primary expertise is the use of econometric and financial modeling methods to assist clients with issues related to capital markets, financial reporting, and financial management. He has 15 years of international experience spanning client engagements in the United States, Brazil, and Southeast Asia. He has published in both academic and professional journals on finance and accounting topics, and has taught courses and presented seminars on finance- and accounting-related topics in major U.S. universities, Germany, and Latin America.

Dr. McLelland can be contacted by e-mail to mmc@mclelland-financial-economics.com.