Understanding IPCPL Theory, Evidence, and Application

Use in Private-Business Valuation (Part IV)

In this fourth article, the authors show how to apply the IPCPL theory using public market cost of capital.

Read Part I, Part II, and Part III

Application of IPCPL Theory

When Bob Dohmeyer, Pete Butler, and Rod Burkert published their article on the IPCPL in 2013, they developed a discount rate from the Deal Stats database. In 2015, we published an article in which we set forth that their incite that the difference between the cost of capital in a public market and private market is largely due to the difference in transaction costs between the two markets was very important in the development of a financial theory relevant to private capital transactions. We then set forth how IPCPL theory is consistent with accepted financial theory in academic circles and can be empirically tested. In the first three articles of this series, we set forth an explanation of IPCPL theory, explain how it is consistent with accepted financial theory, and reviewed empirical studies supporting IPCPL. In this article, we show how to apply the IPCPL theory using public market cost of capital.

Readers of the previous three articles, and readers unfamiliar with those articles, will benefit from the following recap of what those articles are about and what they demonstrate.

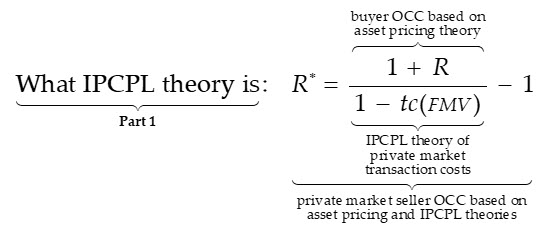
The first article develops the understanding that IPCPL theory provides an explanation and prediction of how transaction costs reconcile the difference between a buyer’s and a seller’s respective opportunity costs of capital (OCC):

An important aspect of this relationship is that the buyer’s OCC is generally determined by the price of risks set under fair market conditions, i.e., in open, competitive capital markets, which are generally only observed in public capital markets. This is important because private capital market transactions are rarely conducted under such conditions, so it is generally unreasonable to assume private capital market transaction data reflect fair market pricing of risks. Under the most basic assumption underlying valuation theory, termed either the law of one risk price or simply the no-arbitrage principle, this means that fair market value (FMV) of privately held capital assets cannot be estimated solely from private capital market data. Indeed, as suggested by the above expression, IPCPL theory implies that the FMV of privately held capital assets can only be estimated from estimates of public market risk prices and private capital market transaction costs.

Part II of this article series develops an understanding of private capital market transaction costs, a general functional form of the relationship between such transaction costs and transaction FMV or price, and the empirical implications of IPCPL theory, i.e., that transaction costs are a decreasing, convex function of transaction FMV or price:

An important aspect of Part II is that the empirical implications of IPCPL theory and the general functional form shown above is that they follow directly from the well-known Lehman formula used in setting capital market transaction fees since the 1970s or 1980s. In this connection, IPCPL theory and its empirical implications simply represent a formalization of intuition derived from the Lehman formula and placed in the context of modern asset pricing theory.

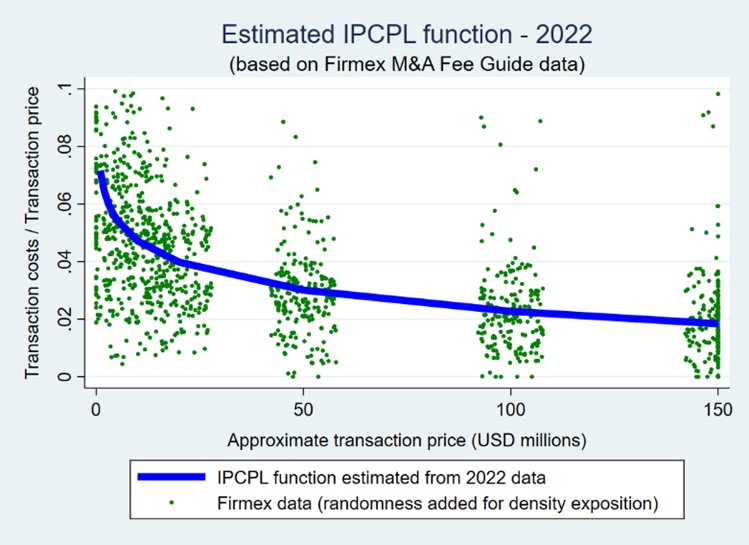
Part III of this article series discussed empirical evidence on IPCPL theory presented by Gorshunov (2015) and Goodman and McLelland (2017), as well as new evidence. The aggregate evidence is essentially all consistent with the empirical predictions of IPCPL theory, and such evidence is based on both private capital market transaction data obtained from DealStats (formerly Pratt’s Stats) for the period 1993 through 2015, and on international data on private M&A transactions obtained from Firmex for the period 2016 through 2022. The most recent evidence presented in Part III represents an IPCPL transaction cost function estimated from the Firmex data for the approximate post-COVID-19 period 2020 through 2022:

Perhaps the most interesting aspect of Part III is the remarkable simplicity of estimating and testing the general form of an IPCPL transaction cost function shown above (which is also consistent with IPCPL theory, as discussed). If private capital market transaction costs and related transaction price data are available, then the IPCPL function can be estimated using the least squares method that is available in most quantitative spreadsheet programs (e.g., Microsoft Excel).

Public capital market data, which is freely available via various websites (e.g., Google Finance and Yahoo Finance), can be used to estimate the fair market price of risks, and private capital market transaction costs can be estimated using freely available transaction data from various financial data service providers (e.g., Firmex[1]). Of course, it is often more efficient to use valuation data providers, but it is not entirely necessary.

In summary, IPCPL theory implies that the FMV of privately held capital assets can be stated—using notation introduced above—in terms of discounted expected cash flows where the discount factor is adjusted for the IPCPL transaction cost function: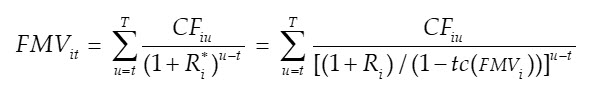

In Part IV, the final article in this series, a simple example of applying IPCPL theory is presented and discussed with the intent of making IPCPL more accessible and easily usable in standard business valuation practice.

 4.1 An Example of Estimating FMV Under IPCPL Theory

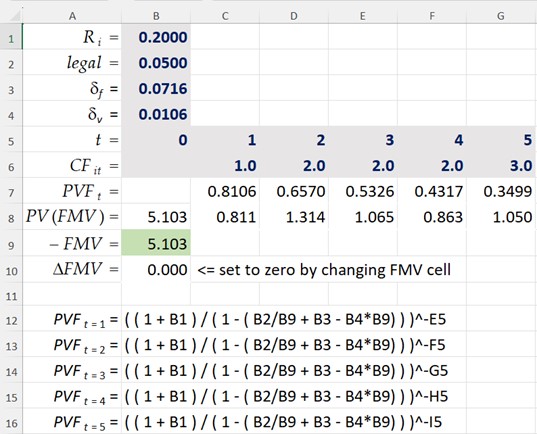
Consider a semi-realistic example of estimating the FMV of a privately held enterprise using the discounted cash flow method at a 12/31/2023 valuation date, where the valuation analyst has already developed accurate reliable forecasts of expected future cash flows consisting of five future cash flows of $1.0 at t=1, $2.0 at t=2,3,4, and $5.0 at t=5 (in millions):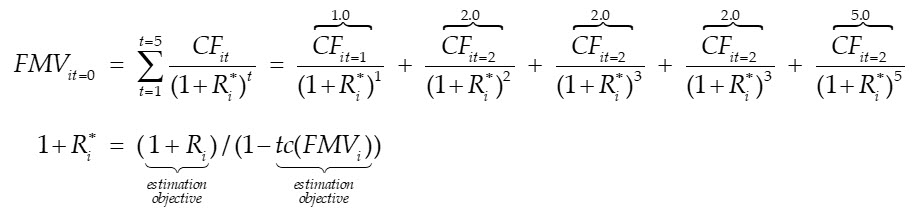

As suggested by the equation showing the details of the risk-adjusted discount rate implied by IPCPL theory, the valuation analyst has two remaining estimation objectives: (i) the fair market risk-adjusted discount rate, R_i (before private market transaction costs), and (ii) the private market transaction cost function implied by IPCPL theory, tc(FMV_i).

4.2 Risk-adjusted Discount Rate

It is helpful to once again recall that IPCPL theory has nothing to do with risk-adjust discount rates per se (i.e., as shown in the first equation at the beginning of this article); the risk-adjusted discount rate and the IPCPL transaction cost adjustment to the discount factor are conceptually distinct. In this connection, for the risk cash flow stream shown in the previous section, we will simply assume the valuation analyst uses a method consistent with existing valuation practice to estimate the risk-adjusted discount rate:

With this estimate, the valuation analyst only needs to estimate the IPCPL transaction cost function and then solve for FMV.

4.3 IPCPL Transaction Cost Function Estimation

The valuation analyst, having read Part III in this article series, chooses to use the same functional form for the IPCPL empirical model to estimate private market transaction costs, but notes such costs seem to be increasing over time. Accordingly, the analyst chooses to use only data from the Firmex M&A Fee Guide 21/22 for transactions circa 2021–2022, rather than the broader sample from 2016–2022 used in Part III of this series.

Using the 2021–2022 data, the most recent data available from Firmex as of this writing, the analyst estimates the IPCPL empirical model again using the regression analysis application embedded in Microsoft Excel spreadsheet software: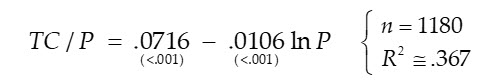

The small p-values shown below the parameter estimates (in parentheses) indicate the model is reliably estimated and—as also shown in the graph below—the parameter signs are consistent with empirical implications of IPCPL theory, i.e., transaction costs are a decreasing, convex function of transaction price (or FMV):

Then as suggested in Section 3.4 of Part III of this series, perhaps based on an informal survey of corporate attorneys, the valuation analyst estimates a base level of legal and other profession fees (e.g., valuation services fees) associated with selling an enterprise of similar complexity to the subject interest to be $50,000 ($ .05 million). With this estimate and the IPCPL function estimated from the 2021–2022 data as shown above, the adjusted transaction cost function would be: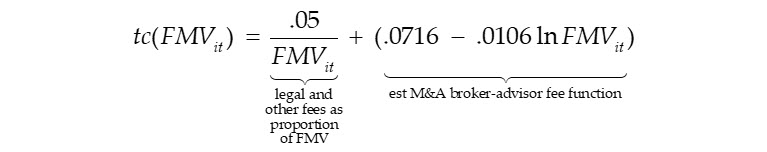  

The analyst has now obtained the estimates for risk-adjusted rate of return and transaction costs necessary to solve for FMV of the subject enterprise:

4.4 Solving the Non-linear Equation for FMV

Inserting the expected cash flows, the estimated risk-adjusted discount rate, and the estimated adjusted IPCPL function, into the discounted cash flow model results in:

The above expression is a non-linear equation with a single unknown variable: FMV_it=0. Noting that the right-hand side of the above equation is simply a present value expressed as a function of the unknown variable, PV(FMV_it=0), the following equation represents the basic condition used to solve the non-linear equation using numerical methods such as is available in Microsoft Excel’s Goal Seek application: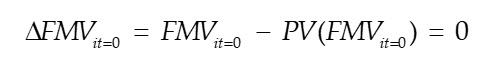

Inserting the expected cash flows and estimated valuation model parameter values into a present value expression implemented in Microsoft Excel, the valuation analyst uses Microsoft Excel’s Goal Seek method to solve for estimated FMV of the subject enterprise:

So, the estimated enterprise FMV at the valuation date is: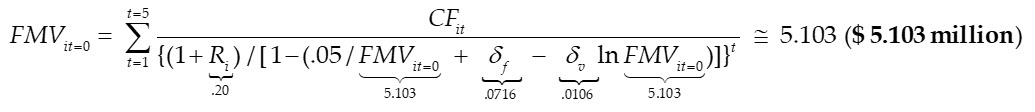

Finally, it is helpful to see what the IPCPL-adjusted, risk-adjusted discount rate is in comparison to the 20.0% unadjusted rate discussed in Section 4.2: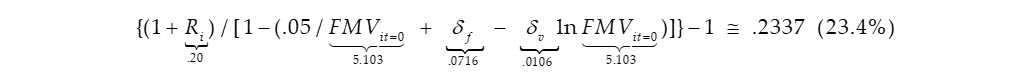

So, to recapitulate, the valuation analyst (i) estimated the expected future stream of risky cash flows; (ii) estimated a risk-adjusted discount rate representing the fair market price of risk(s); (iii) estimated the IPCPL transaction cost function adjusted, if necessary, for legal and other professional fees associated with the hypothetical sale of the subject interest; and finally, (iv) solved for the enterprise FMV at the valuation date.

4.5 Final Thoughts

To summarize this series, it is helpful to recall the history of IPCPL theory and methods. The series has demonstrated that IPCPL theory and methods, first introduced in the early 2010s, are derived from substantial professional experience in private capital market transaction advisory services. The intuition coming from such experience led to implementing basic IPCPL theory using the well-known Lehman formula, which represents an approximation of private market transaction costs because it was—and perhaps still is—the most widely-used method of setting capital transaction advisory and brokerage fees.

IPCPL theory was formalized and empirically tested beginning in the mid-2010s. The literature reflecting such theory and evidence—including this series of articles—has demonstrated the following: (i) transaction costs represent the critical link between public capital market risk pricing and private capital market transaction prices and FMVs; (ii) capital asset transaction costs are logically a decreasing, convex function of transaction price or FMV; and (iii) substantially all empirical evidence using data spanning the 1993–2022 period is consistent with the empirical implications of IPCPL theory.

With this history in mind, we will end this series with what we think is the most succinct way to state the importance and usefulness of IPCPL theory and methods:

IPCPL theory implies private capital market transaction costs represent the shadow price of liquidity risk in private capital markets, i.e., the price of liquidity risk where it traded explicitly in private capital markets. Such theory is well-grounded in valuation theory and the underlying asset pricing and financial economic theories. IPCPL theory has been empirically tested and is easily testable by any valuation analyst.

[1] Firmex publishes a free annual study: https://www.firmex.com/resources/reports-guides/global-ma-fee-guide-24/

---

David Goodman, MBA, CPA, CVA, has 25 years of experience in performing business valuations and forensic accounting services for family law and business disputes. He also has prepared business valuations for tax and buy-sell purposes. He has an MBA from the Amos Tuck School at Dartmouth College. He is a past-president of the NACVA-Mass State Chapter, past chair of the Massachusetts Society of Certified Public Accountants Litigation and BV committee, and a past board member and treasurer of the Massachusetts Collaborative Law Council. As a financial neutral, Mr. Goodman has helped divorcing couples reach peaceful equitable solutions. He has presented on business valuation and tax issues related to divorce at NACVA annual conference, NACVA-Mass. State Chapter, and the Massachusetts Collaborative Law Council. He has also testified as an expert witness in court and arbitration. He is currently serving on the editorial board of QuickRead.

Mr. Goodman can be contacted at (617) 698-3950 or by e-mail to dgoodman@joacpa.com.

Malcolm McLelland, PhD, has 40 years of professional and academic experience in finance and accounting, including positions in commercial banking, consulting, and educational institutions. His primary expertise is the use of econometric and financial modeling methods to assist clients with issues related to capital markets, financial reporting, and financial management. He has 15 years of international experience spanning client engagements in the United States, Brazil, and Southeast Asia. He has published in both academic and professional journals on finance and accounting topics, and has taught courses and presented seminars on finance- and accounting-related topics in major U.S. universities, Germany, and Latin America.

Dr. McLelland can be contacted by e-mail to mmc@mclelland-financial-economics.com.