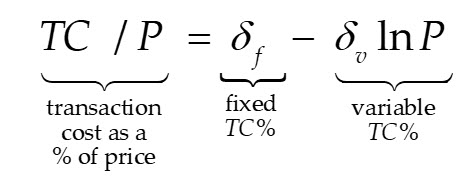Understanding IPCPL Theory, Evidence, and Application
Use in Private-Business Valuation (Part II)
This article in this continuing series explains the Implied Private Company Pricing Line (IPCPL), theory, evidence, and application of the IPCPL.
How to Understand IPCPL Theory
In the first article in this series (published in two parts 02/01/24 and 02/08/24), it was shown that the Implied Private Company Pricing Line (IPCPL) theory explains and predicts the relationship between a capital asset seller’s opportunity cost of capital (OCC) and a buyer’s OCC. That difference is attributable to transaction costs, which is assumed to be a function of the fair market value (FMV) of the capital asset; as shown in Section 1.5 of Part I.
In this article, Part II, we present how to understand IPCPL theory in terms of business valuation theory and financial economic theory, both of which would be generally familiar to business valuation professionals. In particular, we show a methodology for estimating transaction costs in a private fair market.
2.1 A Review of IPCPL Concepts
Unobservable Private Market FMVs and Transaction Costs
The IPCPL theory is based upon the no-arbitrage principle. Recall, that the no-arbitrage principle is a fundamental concept in finance that states that there should be no risk-free opportunities to make a profit. In other words, if there is a way to make a profit without taking any risk, then investors will take advantage of this opportunity until it is no longer profitable. This will cause the prices of assets to adjust until there are no more arbitrage opportunities. Therefore, essential to IPCPL is the concept that buyers are pricing risk; their opportunity cost of capital. The value of the business is a function of the expected cash flows and the buyer’s opportunity cost of capital.
Thus, fair capital markets (open, competitive markets) represent trading of risks rather than trading of capital assets per se. Both CAPM and arbitrage pricing theory suggest that trading of capital assets is largely a byproduct of trading risks because, for example, there is no reason in principle to trade two assets of equal risk.
The common definition of FMV is the price at which property would change hands between a hypothetical willing and able buyer and a hypothetical willing and able seller, acting at arm’s length in an open and unrestricted market, where neither is under compulsion to buy or sell, and when both have reasonable knowledge of the relevant facts. This definition is, in fact, incomplete because it fails to address transaction costs. The International Valuation Standards Council clarifies the FMV concept by stating:
[Fair market] value is the estimated exchange price of an asset without regard to the seller’s costs of sale or the buyer’s costs of purchase and without any adjustment for any taxes payable by either party as a direct result of the transaction. (IVS Framework, 2014, paragraph 36)
The IVS-augmented definition of FMV is the source for the expression (shown in our first article) showing the relationship between observable market prices and unobservable values under the no risk arbitrage condition.
Consider two assets, M and N, that are identical in terms of risks and an expected cash flow of $1, with the only difference being that M trades in a fair public market and N is privately-held and will be traded in a private market transaction. Because assets M and N both (i) have identical risk exposures, sensitivities, and expected cash flows, and (ii) trade in fair markets—implying the existence of the no risk arbitrage condition—it follows that the only difference between the FMVs is attributable to the transaction costs differential between the two markets.
This equation shows why IPCPL is necessary. Neither FMV nor private market transaction costs for asset N are observable; only the public market price of the identical asset M is observable. This represents one equation with two unknowns, implying that either the FMV or the transaction costs for asset N must be estimated. For several reasons, in the general case where assets M and N are not identical, it is substantially easier to empirically estimate transaction costs in the private market. This is what IPCPL does.
Private Capital Market Transaction Prices
It is important to be clear about the specific relationship between FMVs set in public versus private capital markets—which depends critically on transaction costs—and on the relationship between FMV and observable price in private capital market transactions. So, what theory (other than IPCPL) explains and predicts how buyers and sellers set observable prices in such private market transactions? To answer the question, it is helpful to first consider what existing valuation literature says about transaction costs.
Although other texts in the business valuation literature are largely silent with respect to transaction costs, the International Valuation Standards Council (International Valuation Standards, 2017, p. 28) states:
Transaction Costs
Most bases of value [including fair market value] represent the estimated exchange price of an asset without regard to the seller’s costs of sale or the buyer’s costs of purchase and without adjustment for any taxes payable by either party as a direct result of the transaction.
The basic rationale for the general exclusion of transaction costs from valuation estimations can be seen in a discussion of fair value under U.S. accounting standards (Hitchner, 2017, p. 936):
Transaction costs are specific to the transaction and represent the incremental direct costs to sell the asset … ; thus, the price should not be adjusted for transaction costs, because they are not an attribute of the asset … .
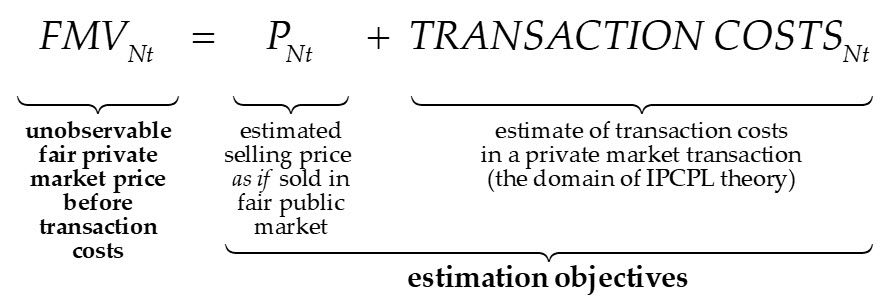
The above definitions suggest that FMV and fair value valuation bases are independent of transaction costs. Existing financial economic theory, however, suggests such costs do indeed influence observed and observable transaction prices because investors have the choice to exchange their available liquidity for risk assets in either public or private capital markets. Then because risk prices must be equivalent under the no-arbitrage assumption, with only transaction costs differing across the markets, it follows that FMV in a private market transaction is necessarily equal to the FMV estimate of the business as if it were traded in the public capital markets from which the relevant market data is obtained plus private market transaction costs for the business. Considering, again, privately-held and -traded asset N from the example above, this would be written as follows:
The expression implies that if the unobservable fair private market price before transaction costs (FMV) of any subject asset N cannot be estimated from available private market transaction data, then the FMV estimate must be based on a combination of public capital market price data and an estimate of private capital market transaction costs, which is the domain of no coherent theory in the valuation literature other than IPCPL theory.
Existing DLOM Estimation Methods Do Not Suffice
Valuation professionals would perhaps assert a discount for lack of marketability (DLOM) estimated under existing (subjective) methods adequately accounts for the transaction costs differential between public and private market prices; implying IPCPL is not necessary; existing methods are adequate. And yet, with respect to controlling interest DLOMs which represent the least difficult DLOM estimation conditions, Hitchner (2017, p. 422) writes: “Many analysts believe that discounts for lack of marketability or liquidity for controlling interests generally range from 0 to a high of 20 percent, depending on the specific facts and circumstances and the valuation method employed.” Indeed, this statement itself suggests at least some ambiguity with respect to existing DLOM estimation methods where it refers to either “marketability or liquidity.” Consider again statements from Hitchner (2017, p. 395):
… liquidity and marketability are not necessarily the same:
Liquidity: The ability to quickly or readily convert property … to cash … without significant loss … and without significant cost.
Marketability: The ability to quickly convert property … to cash at minimal cost that reflects the capability and ease of transfer or salability … .
The definitions do not clearly imply that either liquidity (“… without significant loss … or cost”) or marketability (“… at minimal cost …”) reflect transaction costs and, therefore, seem to suggest liquidity and marketability discounts reflect risks. To the extent DLOM represents risks rather than transaction costs, DLOM estimation methods—such as they are—do not mitigate the need for a theory addressing private market transaction costs.
So, the discussion here, in combination with the absence of a clear DLOM estimation method being presented in Hitchner (2017), suggests existing DLOM estimation methods do not represent a coherent explanation or prediction of why asset prices differ between public and private market transactions. In contrast, as will be seen later in this series, IPCPL theory provides a clear, empirically testable explanation and prediction of how and why asset prices differ between public and private markets; and that explanation has to do with private market transaction costs.
2.2 The Intuition of IPCPL Theory
Perhaps the easiest way to understand IPCPL theory is to understand the FMV estimation problem from the perspectives of Bob Dohmeyer and his co-authors, Pete Butler and Rod Burkert, circa 2012 (“DBB”). Private conversations with these originators of IPCPL indicate that the primary insight underlying IPCPL theory was the following idea, stated concisely in terms of modern asset pricing theory as follows:
Public capital markets are (usually) accurately characterized as open, competitive, highly liquid markets for trading risks, where transaction costs are negligible. In contrast, private capital market transactions are often characterized by non-open, non-competitive negotiations (usually) intermediated by brokers and advisors who charge significant fees representing transaction costs incurred to facilitate trading of risks; and, as such, the transaction costs represent the price paid for accessing liquidity.
This insight comes from the IPCPL originators’ experience in private market M&A transactions, where they noticed the following:
(i) Â Â Buyers of privately-owned businesses tend to represent the class of buyers of privately-held businesses that are willing to pay the highest price and, so, generally represent the most relevant buyers in determining FMV, and so are the most relevant in terms of estimating OCC for private capital market transactions.
(ii)Â Â Such buyers tend to set bid prices for private market acquisitions based on estimates of OCC based on public market returns to risk and, so, the OCC used in setting the private market transaction prices generally represent fair market risk-adjusted expected rates of return.
(iii)Â Such buyers tend to adjust their bid prices for private market acquisitions downward based on their estimated transaction costs, so as to effectively achieve the same risk-adjusted return to risks that they would obtain in their own companies in the public equity markets.
A reasonable interpretation of DBB’s insights is that buyers are essentially exchanging liquidity—that would otherwise be used to acquire risk exposures in the public markets—for less liquid risk exposures available in privately-held assets.
It also follows that if transaction costs are necessarily required in association with publicly-held buyers’ exchanging liquidity for privately-held risk exposures, then such private capital market transaction costs represent what economists would term the private market shadow price of liquidity risk; the theoretical price of liquidity risk in the private capital market if it were being explicitly traded. This is a remarkable and entirely original insight of DBB, for which the business valuation profession will one day—we predict—realize is of critical importance to business valuation theory and practice.
2.3 Transaction Cost Function Estimation Under IPCPL Theory
Recalling that transaction costs are, in general, unobservable, it follows that the costs must either be estimated or assumed; with estimated being the preference for several reasons. In this section, the intuition and related theory of private capital market transaction costs are outlined, and this theory represents a critical element of IPCPL theory.
Lehman Formula Transaction Advisor Fees
Also based on private market M&A transactions experience, DBB had the insight that perhaps the most common, general method of determining the bulk of fees paid to transaction brokers and advisors is called the Lehman Formula; named after the investment banking firm Lehman Brothers. Stated in natural language, the original formula is:
5% fee for the first $1 million of transaction price
4% fee for the next $1 million of transaction price
3% fee for the next $1 million of transaction price
2% fee for the next $1 million of transaction price
1% fee for transaction price exceeding $4 million
Over time, the fee percentages (f i %) and the transaction price increments (PI i) have both changed, on average, and tend to vary widely. To represent the Lehman Formula in more general natural language form, this can be written as:Â
f1 % fee for the first PI1 of transaction price
f2 % fee for the next PI2 of transaction price
f3 % fee for the next PI3 of transaction price
f4 % fee for the next PI4 of transaction price
f5 % fee for transaction price exceeding PI1 + PI2 + PI3 + PI4
Linear General Case
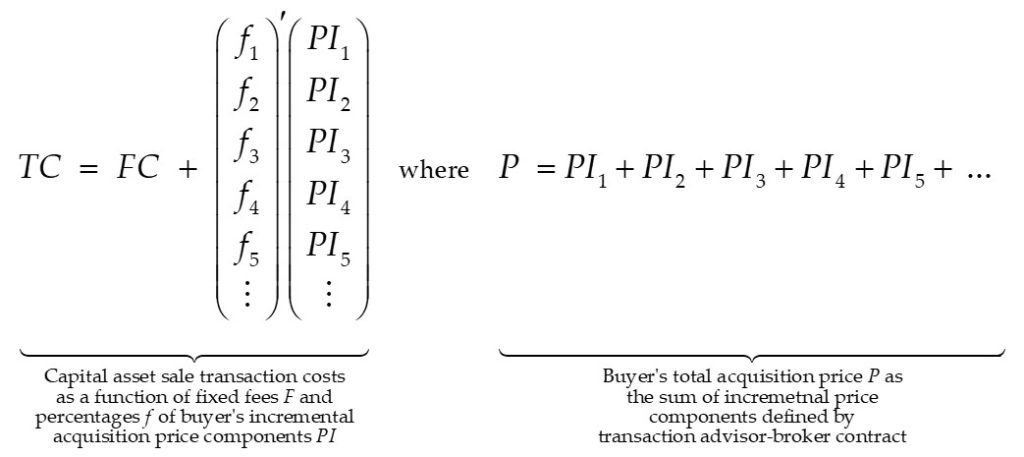
Because all transaction broker-advisor contracts are, of course, negotiated, it is also the case that more general forms including more transaction price increments exist in practice. In mathematical notation, a general form of a Lehman Formula with the addition of fixed transaction fees and costs (FC) (i.e., fees that do not vary with the transaction price) can be written as follows:
Linear Special Case
In the original presentation of IPCPL theory, DBB used a special case of the above Lehman Formula as a transaction cost estimation function; specifically, DBB used what is usually called the Double Lehman Formula, which in terms of the above general formula would be written as:
In this Double Lehman Formula with added fixed transaction fees, it is our understanding that DBB estimated the fixed cost component (FC) using a numerical method, which is discussed in general terms in Goodman and McLelland (2017).
The choice of this special case of the Lehman Formula in DBB—also representing a special case of a transaction cost estimation function—was reportedly based on a qualitative assessment that this version of the formula corresponded most closely to transaction costs that DBB encountered in the small end of the private capital market.
A Simple Non-Linear Transaction Cost Function
In the formal mathematical development of IPCPL theory presented in Goodman and McLelland (2017), a simple non-linear transaction cost function was used; specifically, transaction cost (TC) as a percent, or proportion, of transaction price (P) as a function of the natural logarithm of transaction price (ln P).
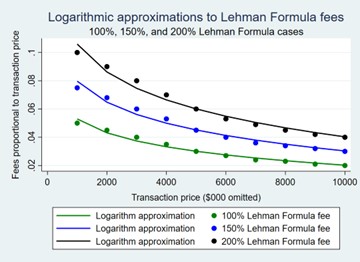
This non-linear function is a simple, reasonably comparable, continuous function that is quite similar to the discrete, linear Lehman Formula. To see this, consider the following graph showing the logarithmic function fitted to three different versions of the Lehman Formula using the least squares estimation method.
The graph shows that the logarithmic function (i) fits the Lehman Formula fairly closely, explaining about 95% of the variation in Lehman Formula fees, and (ii) can be used to estimate a transaction cost function from actual private market capital market transaction data (e.g., DealStats) representing what buyers and sellers actually do in the real world.
An important implication of the logarithmic function is that it can be used to simultaneously (i) empirically test the Double (200%) Lehman Formula assumed by DBB and, more importantly, (ii) to directly estimate the average transaction cost function used in private capital markets from available private capital market transaction data. The decreasing, convex form of a private market transaction cost function—properties of both the Lehman Formulas and the logarithmic function—was explained and predicted in Goodman and McLelland (2017).
2.4 Why IPCPL Theory Works
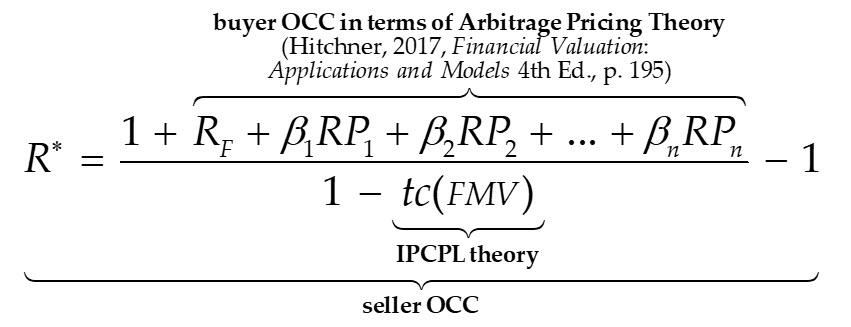
With respect to private capital market risk pricing irrelevance to IPCPL theory, it is only necessary to understand the expression for the seller’s OCC under IPCPL theory; the derivation of which was outlined in Part I of this article series and presented in the introduction to this article, Part II; abbreviated here for conciseness as follows:
The expression shows the logical relationship between a buyer’s and a seller’s OCC, under the no-arbitrage assumption and IPCPL theory. Importantly, this expression shows how modern asset pricing theory—which most valuation professionals would normally associate with a buyer’s OCC estimated from public capital market data—reconciles with how a seller would optimally estimate OCC in a fair private capital market. If the valuation objective is to estimate the FMV of a privately-held entity, then it follows from the fundamental no-arbitrage risk pricing assumption underlying all modern asset pricing theory that public capital market data can be used to estimate risk prices; both for publicly-traded and privately-held assets. IPCPL theory and related private capital market transaction cost estimation methods provide the formal explanation and prediction of the relationship between public and private capital markets.
In summary, IPCPL theory is consistent with modern asset pricing theory (e.g., arbitrage pricing theory). The Lehman Formula in its general form is not artificial but, rather, is commonly—though perhaps not widely—used in private capital market transactions. Rather than intending to explain and predict how risk is priced in private capital market transactions, IPCPL theory explains and predicts how private market transaction costs influence asset prices and OCC, which are otherwise explained and predicted by modern asset pricing theory.
2.5 Future Issues
In the remaining articles in this series, we will address the following questions with respect to IPCPL theory and methods:
Part III—What is the evidence supporting IPCPL theory?
Part IV—How can IPCPL be applied in practice?
David Goodman, MBA, CPA, CVA, has 25 years of experience in performing business valuations and forensic accounting services for family law and business disputes. He also has prepared business valuations for tax and buy-sell purposes. He has an MBA from the Amos Tuck School at Dartmouth College. He is a past-president of the NACVA-Mass State Chapter, past chair of the Massachusetts Society of Certified Public Accountants Litigation and BV committee, and a past board member and treasurer of the Massachusetts Collaborative Law Council. As a financial neutral, Mr. Goodman has helped divorcing couples reach peaceful equitable solutions. He has presented on business valuation and tax issues related to divorce at NACVA annual conference, NACVA-Mass. State Chapter, and the Massachusetts Collaborative Law Council. He has also testified as an expert witness in court and arbitration. He is currently serving on the editorial board of QuickRead.
Mr. Goodman can be contacted at (617) 698-3950 or by e-mail to dgoodman@joacpa.com.
Malcolm McLelland, PhD, has 40 years of professional and academic experience in finance and accounting, including positions in commercial banking, consulting, and educational institutions. His primary expertise is the use of econometric and financial modeling methods to assist clients with issues related to capital markets, financial reporting, and financial management. He has 15 years of international experience spanning client engagements in the United States, Brazil, and Southeast Asia. He has published in both academic and professional journals on finance and accounting topics, and has taught courses and presented seminars on finance- and accounting-related topics in major U.S. universities, Germany, and Latin America.
Dr. McLelland can be contacted by e-mail to mmc@mclelland-financial-economics.com.