Demystifying Monte Carlo Simulation

Time to Revisit this Tool

If you think Monte Carlo simulations are too complex to use in business valuation, you are not alone. There are three main reasons valuators shy away from using Monte Carlo analysis: 1) they do not totally understand it, 2) it involves statistical analysis and most would prefer not to relive their college statistics class, and 3) it is difficult to explain, especially to a jury. A recent survey by Business Valuation Resources (BVR), which was ongoing as of the date this article was written, indicates 51 percent of the respondents (82 respondents to date) use Monte Carlo simulations and of those, 51 percent use them for “select valuations as needed,” while another 34 percent used them infrequently for specific projects. Only 15 percent indicated they used them in nearly all valuations. This article is a primer on the use and value of Monte Carlo simulations.

If you think Monte Carlo simulations are too complex to use in business valuation, you are not alone. There are three main reasons valuators shy away from using Monte Carlo analysis: 1) they do not totally understand it, 2) it involves statistical analysis and most would prefer not to relive their college statistics class, and 3) it is difficult to explain, especially to a jury. A recent survey by Business Valuation Resources (BVR), which was ongoing as of the date this article was written, indicates 51 percent of the respondents (82 respondents to date) use Monte Carlo simulations and of those, 51 percent use them for “select valuations as needed,” while another 34 percent used them infrequently for specific projects. Only 15 percent indicated they used them in nearly all valuations.¹

According to the survey, the reasons why the other 49 percent do not use Monte Carlo are as indicated above, or because clients did not want or need that type of analysis. While those are all understandable reasons, Monte Carlo simulations can provide a lot of value in certain situations, which is why I will attempt to demystify it using some simple examples.

What is a Monte Carlo Simulation?

Simply put, it is the computer generation of multiple scenarios using a variable or set of variables as input. Once the computer has run multiple iterations (hundreds, thousands, or millions of possible scenarios), the analyst can then apply statistical analysis to determine the most likely outcome for the value being sought.

What Monte Carlo is NOT

I often hear the term “Monte Carlo method.” To be clear, using Monte Carlo simulations is not a method, per se, as the term is defined in the business valuation world. It is an analysis tool or technique, much as we use Excel what-if scenarios as a tool and the binomial lattice as a technique.

It is also not just a more complicated form of probability analysis when the analyst has fairly good estimates of the probabilities of certain outcomes. For example, say an analyst has four cash flow forecasts based on predictions of what will happen with the economy as the U.S. continues to deal with COVID-19. The first cash flow estimate assumes the economy continues to implode, the second anticipates a slightly better but still sluggish economy, the third is an estimate if the economy is slowly recovering, and the fourth is a best-case scenario in which the economy is recovering faster than expected. The analyst believes the probabilities are as follows: scenario one (20 percent likely), scenario two (40 percent likely), scenario three (30 percent likely), and scenario four (10 percent likely). This is a very straightforward proposition involving weighting the various cash flows, but what if the analyst is less certain about the likelihood of each scenario occurring?

Monte Carlo simulations, by contrast, perform statistical analysis of the entire data set of outcomes and each trial (iteration/outcome) is assigned equal weight. If a certain outcome is more probable than other outcomes, then that outcome should occur in more trials. So, instead of the probability being assigned upfront, as it is in the previous example, the probability of a particular outcome is given by the frequency of it occurring within the distribution of possible outcomes.

Simple Example

If we roll two dice, each one has six possible discrete values ranging from one to six. Since there are two dice, each with six possible values, the total number of combinations is 36 (6 x 6). Say we want to figure out the probability of rolling a combined seven. There are six possible combinations to get a seven: 1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2, and 6 + 1. Thus, the probability is 6/36 or 16.67 percent that any individual roll will yield a seven.

Because the dice example is a simple problem from a statistical calculation perspective, using Monte Carlo simulations is not advantageous. However, if we did program a computer to solve the math for us, the computer would simulate rolling the dice as many times as we told it to do so. We would tell the computer the variables are two dice with six possible discrete values ranging from one to six. The computer would then run the simulations with randomly generated numbers contained within the specified range of possible values and give us an expected value. The more simulations run, the closer the expected value produced should be to the correct expected value. So, Monte Carlo is nothing more than a way to use repeated simulations to arrive at the most probable outcome based on a particular set of inputs. Using Monte Carlo simulations to model free cash flow inputs might result in a probability distribution output similar to the graph below, which depicts a normal distribution.²

Sample Monte Carlo Simulations Output—Discounted Cash Flow²

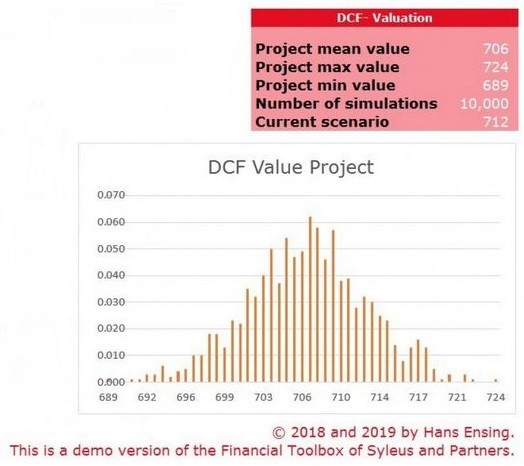
Again, the more trials that are conducted, the less variability there should be in the results and the closer the mean (average) should be to the correct expected result. This can be proven by comparing the results of Monte Carlo simulations that vary only in the number of trials run. In the case of the two dice, here are the results of 100 rolls vs. one billion.³

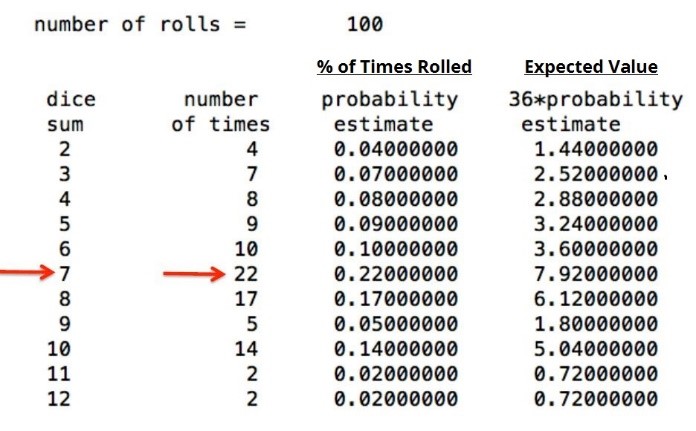
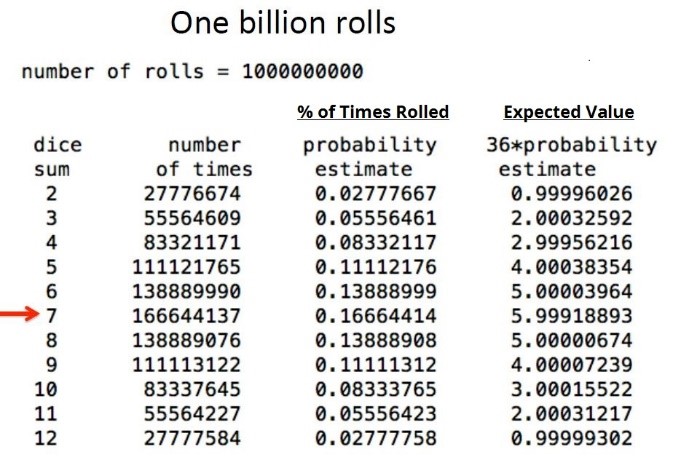
Key Steps Required to Use Monte Carlo for Discounted Cash Flow Simulations

• Load the historical data and determine all the variables relevant to your particular valuation. For example, key variables might include growth assumptions, forecasted sales levels, variable cost percentages, tax rates, capital expenditures, working capital, etc., to arrive at the forecasted free cash flow.
• Analyze the historical data for patterns to determine how different variables are interrelated; for example, as sales go up, the company may be able to negotiate better purchasing terms and lower its cost of goods sold as a percentage of sales. These relationships would be the correlation assumptions. Remember to use your judgment as to how these relationships may change in the future, especially if the company’s future environment is expected to differ from the past.
• Determine the type of distribution you should expect for each variable. These can be continuous, which means the randomly generated value can be any value within the distribution (e.g., a normal distribution), or discrete, where the random values are chosen from two or more specific scenarios. In the case of the dice, each die would have six possible discrete values: 1, 2, 3, 4, 5 and 6.

Graphs taken from the Forecaster’s Toolbox: How to Perform Monte Carlo Simulations⁴

Normal distribution

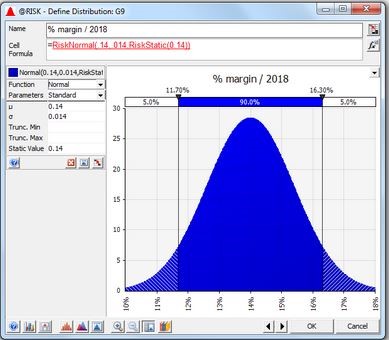
Discrete with two possible values

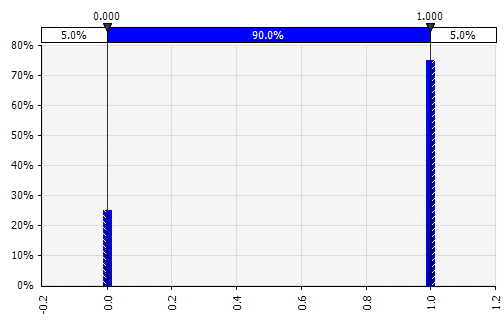
• Set any lower or upper limits for each variable; for example, you might assume that $100,000 in sales will be the lowest expected level of sales and $600,000 will be the highest. In the dice example, the range would be one to six for each die.
• Set the number of iterations the computer will generate. Remember, the more iterations, the closer the mean should be to the actual expected value.
• Run the program and analyze the results. Typically, in a normal distribution, the mean (average) will be the expected value.

When you consider all the factors that go into calculating free cash flow projections: sales estimates, variable expense percentages, fixed costs, working capital, capital expenditures, tax rates, revenue growth rates and other factors, and then try to figure out how changes in each factor will affect the other factors, you can quickly get beyond the limitations of a standard Excel model in incorporating all that complexity. Monte Carlo simulations allow you to specify the variables, the relationships between variables, and then let the computer run simulations using random numbers from within the range and specified distribution pattern of each variable—thousands or even millions of times.

Keep in mind that certain variables like growth rate may vary greatly between the short-term and long-term forecasts. This is especially true when there is great uncertainty in the short-term or when you are valuing a startup company. In these situations, you may want to use Monte Carlo for just the short-term scenarios or generate a separate set of scenarios for the long-term.

Dr. Jonathan Kinley in a paper entitled “A New Approach to Equity Valuation,” had an interesting suggestion: rather than trying to discern an accurate rate to discount projected cash flows, it may be more appropriate to embed the risk in the cash flow simulations via probability analysis (as in Monte Carlo simulations) and use the risk-free rate as the discount rate. To date, I have been unable to find the entire paper to explore this further, but I can see where that approach may have merit, especially in unprecedented times such as these.⁵

Most Appropriate Uses  

Although the case can be made for using Monte Carlo in a standard valuation if there are a lot of inputs with a high degree of potential variability, there are times when a Monte Carlo simulation may not only be useful, but necessary; for example, consider a derivative where its value is dependent upon the underlying stock or some other type of security, or where an outcome is contingent upon certain events occurring. These cases usually fall into one of three categories: 1) contingent or conditional outcomes, 2) path-dependent outcomes, and 3) non-linear outcomes.⁶

• Contingent or conditional outcomes are dependent on certain events or results triggering them. A great example of this is an earn-out provision where the payout is dependent upon the company hitting a specified earnings target. Another example would be the use of differing interest rates based on the debt to equity ratio.
• Path-dependent outcomes are dependent on certain results or performance over time; thus, the path determines the outcome. Stock options often vest due to a combination of performance and the passage of time, so their value is not determined by one factor as of the date of the award.
• Non-linear outcomes deal with situations where the downside potential may be far greater than the upside potential, or vice versa. All-or-nothing situations fall into this category as well. If the exercise price of a call option for stock remains above the price at which the stock is trading, it has zero value. It only starts to have value when the stock price rises above the exercise price. Beyond that point, the value is linear with respect to the underlying stock, but prior to that point, it is non-linear.

Here are indications that Monte Carlo simulations may be helpful or even required:

• When there are many variables that affect the outcome, especially if those variables are highly correlated (either positively or negatively) and have a wide range of potential values.
• There is a high degree of potential volatility associated with all or most of the variables.
• When the variables have non-normal distributions (like the examples in the previous paragraph).
• When doing a company valuation where there are many unknowns:
  • Any time there is a lot of risk because of the life cycle stage of the company. Startups are particularly hard to value because of the lack of a track record upon which to base cash flow projections.
  • For companies in certain industries, like high-tech industries where the technology is new and unproven, or where the payoff is potentially huge but so is the risk of failure and bankruptcy.
  • For companies facing class action lawsuits threatening the company’s continued existence.

Monte Carlo simulations are also useful for doing basic sensitivity analysis to determine which variables have the most impact on the outcome and to what degree.

Limitations

An accurate model is needed. Just because an analysis uses complex statistical modeling does not mean the outcome is any better than a simple what-if analysis weighted by probability of occurrence. If the underlying economic model is not well-thought-out, that is, the variables accurately assessed along with the right distribution patterns chosen and appropriate upper and lower limits specified (if applicable), and the correct correlation between variables defined, the statistical output will be useless. It is the proverbial garbage in, garbage out adage.

Overestimating precision/Misinterpreting results. Because of the sophistication of Monte Carlo modeling, there is a tendency to assume the accuracy is much greater than it may be. It is still based on human assessments and the analyst’s best estimates of the degree of risk involved. Moreover, complex statistics are often used incorrectly. As Mark Twain famously said, “There are three kinds of lies: lies, damn lies, and statistics.” Before interpreting any results, spend some time revisiting basic statistical concepts like mean, median, standard deviation, confidence levels, skewness, and kurtosis. (See the AIRA Journal article for a short refresher on statistical terms.)

Complexity and time required. For simple business valuations where the company’s cash flow has followed a predictable linear trend line and the industry and economy are stable, the results may not vary much between the mean statistics generated by Monte Carlo simulations and those resulting from the use of static formulas based on the means of the underlying variables. Considering the complexity and time required for Monte Carlo simulations, utilizing less complex valuation models may be preferable in these cases. 

Available Software

The basic Excel program can be used for simple Monte Carlo simulations but trying to build a complex Monte Carlo simulation model is not recommended for the average Excel user. While I include links for obtaining Excel templates for simple Monte Carlo simulations, I would recommend investigating some of the Excel add-ins that are available: @RISK by Palisade, ModelRisk by Vose, and RiskAMP, all of which make working with Monte Carlo simulations much easier and can be integrated into existing models.⁴

Final Thoughts

This article was written for the roughly half of all business valuation professionals who, according to the interim results of the BVR survey cited earlier, do not currently use Monte Carlo simulations in their valuations. Hopefully, you now understand exactly how Monte Carlo simulations differ from static valuation models and why just weighting different scenarios may not capture all the complexity needed to adequately address the risk inherent in more unstable environments, like the one we are currently experiencing due to the pandemic. Monte Carlo also has the added advantage of forcing the analyst to think through all possible scenarios, even those considered to be remote possibilities.

As I researched all the information and resources available for Monte Carlo simulations, I came across several in-depth examples of applying Monte Carlo to different types of valuations. Rather than re-invent the wheel, I have included both a bibliography for referenced sources as well as an Other Resources section to direct the reader to the application examples and other resources such as downloadable Excel templates that can be embedded into existing valuation models. Except for the second footnote, links to software vendors offering more sophisticated Monte Carlo programs are in a separate section at the end of the listing of other resources.

---

Cathy Roper, CPA, ABV, CVA, CFE, CGMA, is an adjunct professor of accounting at Webster University, a long-time financial professional, and has the rare distinction of being an Elijah Watt Sells medalist when she sat for the CPA exam. Her firm, Roper Consulting Group, is based in St. Louis and specializes in business valuations, lost profits, economic damages, and other types of forensic accounting services. She also partners with ARA Fraud and Forensics in the prevention and detection of business fraud and the quantification of resulting damages.

Ms. Roper can be contacted at (314) 835-7876 or by e-mail to cathy.roper.cpa@roperconsultinggroup.com.

Sources

¹Business Valuation Resources (BVR). (2020) Interim survey results for “Is Monte Carlo becoming a more common business valuation method?” https://www.surveymonkey.com/results/SM-CH6H6W53L/instant

²Ensing, Hans.(2019) “DCF (Discounted Cash Flow) Excel Monte Carlo Simulation Model” https://www.eloquens.com/tool/Kym5uKBM/finance/discounted-cash-flow-dcf/dcf-discounted-cash-flow-excel-monte-carlo-simulation-model (demo and full version software available for sale)

³Booth, Thomas Edward. (2015) “Monte Carlo High School Examples Draft 2” https://www.researchgate.net/publication/279532247_Monte_Carlo_High_School_Examples_Draft_2

⁴Thelin, Stefan. “Forecaster’s Toolbox: How to Perform Monte Carlo Simulations” https://www.toptal.com/finance/financial-forecasting/monte-carlo-simulation

⁵Kinley, Jonathan. (2019) “A New Approach to Equity Valuation” http://jonathankinlay.com/2019/05/a-new-approach-to-equity-valuation/

⁶Beaton, Neil and Sawyer, John. (2019). “Use of Monte Carlo Simulations in Valuation,” AIRA Journal Vol. 32 No. 2, 2019 https://www.alvarezandmarsal.com/sites/default/files/88413_val_monte_carlo_aira_article.pdf

Other Resources—Other Reading/Application Examples/Further Education

Ayres, Douglas, Schmutte, James, and Stanfield, Jason. (November 1, 2017) “Expect the unexpected: Risk assessment using Monte Carlo simulations,” Journal of Accountancy https://www.journalofaccountancy.com/issues/2017/nov/risk-assessment-using-monte-carlo-simulations.html

Lifland, Steven. (2015) “Creating a Dynamic DCF Analysis: A Detailed Excel Approach Utilizing Monte Carlo Methodology,” Journal of Higher Education Theory and Practice Vol. 15(2) 2015, pg 56–66

http://www.na-businesspress.com/JHETP/LiflandS_Web15_2_.pdf

NACVA course, “Monte Carlo Simulation” (prerecorded webinar–1 hr CPE) https://www.nacva.com/store_product.asp?prodid=567

NACVA The Value Examiner May/June 2017, “Monte Carlo Simulation Charts” (lost profits analysis)

https://www.nacva.com/content.asp?contentid=524

Other Resources—Application Examples/Available Software

Frontline Solvers (spreadsheet analytics software) 

https://www.solver.com/monte-carlo-simulation-tutorial

https://www.solver.com/monte-carlo-simulation-overview#What_is_Monte_Carlo_Simulation

https://www.solver.com/risk-solver-platform

ExcelUser (explanation with application examples and a very inexpensive basic Monte Carlo template for Excel)

Article 1 – Introduction to Probabilistic Simulations in Excel

http://www.exceluser.com/reports/introduction-to-probabilistic-simulations-in-excel.htm

Article 2 – How to Create Monte Carlo Models and Forecasts Using Excel Data Tables

http://www.exceluser.com/reports/monte-carlo-models-forecasts-with-data-tables.htm

Palisade’s “Monte Carlo Simulation” (explanation of Monte Carlo including a section on common probability distributions, a free software trial, and free on-demand webinar “Introduction to Risk Analysis Using @Risk”)

https://www.palisade.com/risk/monte_carlo_simulation.asp

@risk Monte Carlo simulation tutorial

https://www.youtube.com/watch?v=KgAHLRxjBsA