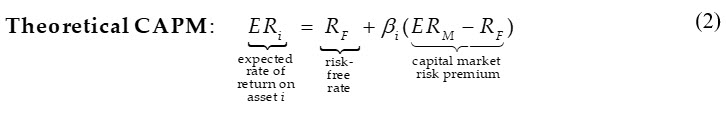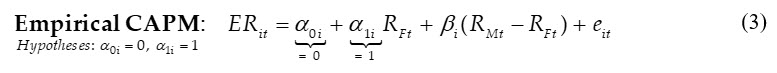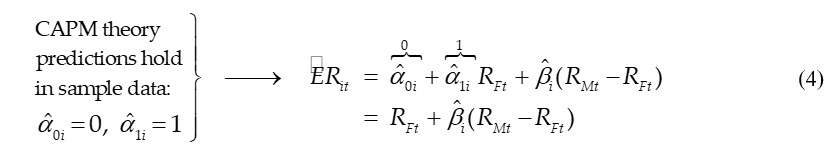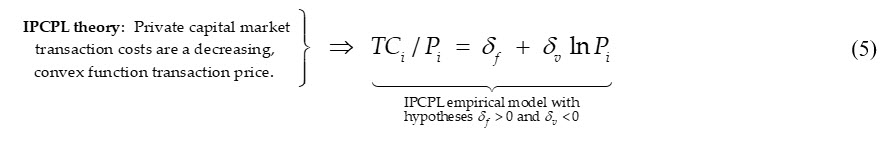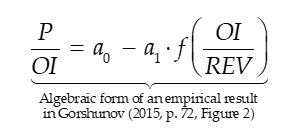Understanding IPCPL Theory, Evidence, and Application

Empirical Evidence Supporting IPCPL Theory (Part III)

In this third article, the authors present the empirical evidence supporting use of the IPCPL theory.

In the second article in this series, it was shown that the general empirical implications of implied private company pricing line (IPCPL) theory are that buyers of privately owned businesses pay higher transaction costs in exchange for higher returns on their investments. The IPCPL theory treats transaction costs (TC) as a proportion or percentage of transaction price (P) stated as a decreasing convex function of P. (The higher the price, the lower the percentage transactions costs are of the selling price.) As also shown in Part II, we can use a decreasing convex function that closely approximates the general functional form of Lehman Formulas commonly used in compensating transaction advisors and brokers in private capital market transactions. This is based on the natural logarithm of transaction price:

This transaction cost function will be used to frame existing empirical evidence on IPCPL theory, and to present new empirical evidence on IPCPL theory as a means of explaining the basic approach to applying IPCPL theory in practice. Specifically, this article will first present the nature of empirical tests of any valuation theory; IPCPL theory included. Existing empirical evidence on IPCPL in the valuation literature will then be discussed, and then new evidence on IPCPL from international private capital market transactions is presented. Importantly, we show that valuation professionals need not wait for valuation data providers (e.g., BV Resources, Kroll, etc.) to provide empirical evidence and data on IPCPL. Any valuation professional can easily develop empirical evidence on IPCPL directly from available private capital market transaction data (e.g., DealStats), as will be further explained in Part IV of this series.

 3.1 Theoretical Models and Empirical Models

CAPM theory and evidence. Before considering empirical evidence on IPCPL theory, it is important to understand the nature and limitations of empirical evidence in general. Consider the following expression for the well-known capital asset pricing model (CAPM) (see, e.g., Hitchner, 2017, p. 194):

While many valuation professionals have some understanding of CAPM and the underlying theory, most are unfamiliar with the nature and extent of the empirical evidence supporting it.

Virtually no theory is expected to hold perfectly in the real world; this is especially true in financial economics because it is well-known there are both rational and irrational buyers and sellers in capital markets. Accordingly, most theories related to capital markets are expected to represent rational buyers and sellers only on average across economic conditions and time. Recognizing this, an empirical model—often referred to as a regression model—for CAPM theory would typically be represented by an expression like the following:

Several elements exist in the empirical CAPM not present in the CAPM theoretical form:

Because the empirical CAPM model is a linear conditional expectation function that reasonably meets certain technical conditions, its parameters can be estimated using least squares estimation methods. Such methods result in the estimated mean value of the model error term (e_it) being zero by adjusting the mean value of the model intercept parameter (a_0i). This results in the expected return being conditional on the estimated values of the other parameters in the model: the marginal effect of the risk-free rate (a_1i) and the marginal effect of the capital market risk premium (b_i, termed CAPM beta).

Denoting empirical model parameter estimates with circumflex accents, it can be seen that if CAPM theory predictions hold in the sample data as reflected in the empirical model, then the empirical data is consistent with CAPM theory as represented in (2):  

An interesting aspect of the above expressions is that the theoretical value of CAPM beta (b_i) is not determined by theory, per se; the theory simply says that expected return is conditional on the expected covariance of the asset’s return with the market return relative to the expected variance of the market return:

This means CAPM beta is determined by its empirical value, rather than by theory. That is, the theory does not explain and predict the value of CAPM beta, it only explains it.

The common view is that because CAPM beta is just an estimate, then CAPM is simply true because, whatever estimate is obtained for beta, it is acceptable under the theory (and, so, in some sense supports the theory). What formulas (3) and (4) show is that CAPM can be quite easily tested by anybody using data from Yahoo Finance and regression analysis in Excel; and either accepted or rejected based on how close the alpha parameters are to 0 and 1.

In this respect, IPCPL theory is like CAPM theory. IPCPL theory only explains that private capital market transaction cost differentials are decreasing convex functions of fair market value (FMV) (or some other variable closely associated with FMV); it does not predict values of parameters of the IPCPL function, which are empirically estimated.

This is all important because IPCPL can be tested, and has been tested, in a similar way to how one might test CAPM. If equity returns are decreasing and convex in any variable that is positively related to FMV or PRICE, then IPCPL is supported by the evidence. But, also like CAPM, the value of the d_v parameter in (5) is not predicted by IPCPL, just the negative sign on the parameter.

IPCPL theory and empirical model. We can model a decreasing convex curve based on IPCPL theory as:

If the empirical data is reliably consistent with the parameter value hypotheses—e.g., d_f > 0 and d_v < 0 in (5)—then there is valid, reliable empirical evidence consistent with IPCPL theory.

3.2 Existing IPCPL Evidence

Early informal evidence. An often-overlooked body of evidence is the informal empirical evidence that leads practicing professionals to form their perceptions and beliefs. The apparent basis for ignoring such evidence is that—unlike evidence based on modern statistical methods and hypothesis testing—it is generally difficult to understand competing hypotheses and the reliability of the evidence.

Nonetheless, informal evidence is important and, in fact, IPCPL theory would not exist without it. Technically speaking, the empirical observations of Dohmeyer, Butler, and Burkert—the developers of IPCPL—that private capital asset transaction prices were decreasing in transaction costs that seemed to approximate some form of the Lehman Formula led to the formal empirical hypothesis that the IPCPL is a decreasing, convex function of the FMV of a privately-held enterprise (or some variable closely associated with FMV). From this perspective, it would be surprising if empirical data were not consistent with this hypothesis; and, all empirical evidence that we are aware of is indeed consistent with the basic predictions of IPCPL theory.

Gorshunov (2015) examined certain aspects of Pratt’s Stats (now DealStats) private enterprise transaction data comprised of 840 transactions spanning the years 1997–2014 and companies (excluding medical doctors’ offices) with between $2.5 and $10 million in revenues. Although not the primary focus of the study and without providing hypothesis test statistics with respect to the empirical predictions of IPCPL shown in (5), Gorshunov shows that transaction-price-to-operating income, P/OI, is an unstated decreasing, convex function of operating profit margin, OI/REV (cf. Gorshunov, 2015, p. 72, Figure 2):

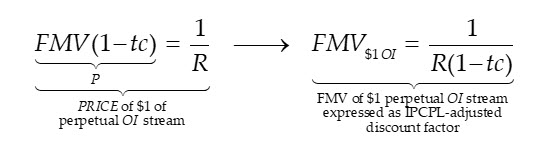
Because the purpose of Gorshunov’s study was only to test certain aspects of private capital market transaction data and not to test formal aspects of IPCPL theory, and it is necessary to rearrange the above result to understand its consistency with IPCPL theory. In this connection, consider the following rearrangement of a Gordon Growth Model suggesting P/OI is (i) conceptually equivalent to a risk-adjust discount factor and (ii) the FMV of a $1 perpetual stream of OI assuming zero transaction costs: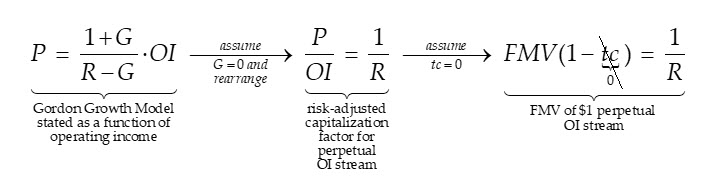

Now consider the above expression without the assumption of zero transaction costs:

This implies the following characterization of Gorshunov’s (2015, p. 72, Figure 2) empirical result and its consistency with IPCPL theory: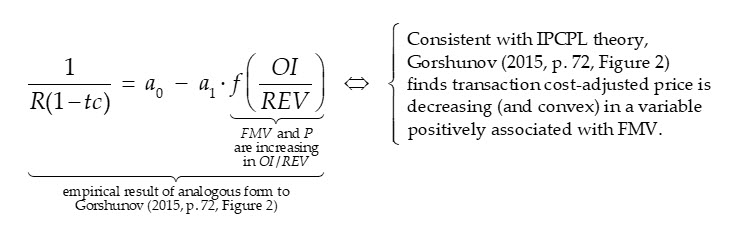

What we are showing here, is that even though Gorshunov did not specifically test IPCPL, his study results are consistent with the IPCPL.

Given the experience and observations of the original developers of IPCPL theory and methods (Dohmeyer, Butler, and Burkert), this empirical result is not surprising; the evidence is just a somewhat more formal presentation of the empirical data, which anticipated the more formal development of the theory in subsequent years.

Goodman and McLelland (2017) presented several empirical models directly derived from IPCPL theory and estimating using data obtained from DealStats (formerly Pratt’s Stats) on 4524 private capital market transactions executed between 1993 and 2015. Because transaction costs are generally not reported in DealStats, it was not possible to construct an empirical model as shown in (1) and, so, it was necessary to derive IPCPL-related empirical hypotheses based on the way in which the estimated risk-adjusted expected rate of return (R_it) was constructed from the DealStats data:

The basic logic underlying the hypotheses is that under IPCPL theory transaction costs as a proportion of transaction FMV (and price) and, therefore, expected all-in expected rate of return is decreasing in both growth and enterprise profits.

Because of heterogeneity in the data—which results in part from the heterogenous 1993–2015 sample period—arguably the most relevant empirical results were derived using the least absolute deviation (LAD) estimation method—a statistical estimation method that is more robust to outlier observations than is the least squares estimation method—of the following model (p-values are shown below each parameter estimate):

The data is consistent with the IPCPL hypotheses on G and EBT, as seen by the negative sign and significant p-values on the parameter estimates but is not consistent with the hypothesis on the interaction term. In simple terms, the implied OCC is a decreasing function based on the size of the transaction. IPCPL predicts that the increased OCC, the smaller the transaction is due to the proportionately higher transaction costs.

It is not clear why a positive sign was found on the interaction term, but it is reasonable to suggest it results from expected EBT growth rate (G) being estimated as the average GDP growth rate in the U.S. economy over the 10-year period ending in the transaction year across all companies in the sample: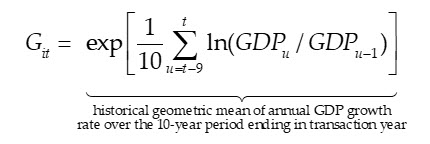

This method of estimating expected future EBT growth was selected for consistency with earlier expositions of IPCPL by Dohmeyer, Butler, and Burkert. Because valuation fundamentally, however, depends on forward-looking valuation inputs, including expected future growth rates, use of historical averages seems likely to bias growth estimates. For this reason, the estimated positive sign on the interaction term parameter is perhaps an artifact of the growth estimation method and a related lack of the necessary data in DealStats to test IPCPL theory.

3.3 New Evidence from Private Mid-market M&A Transactions

As discussed, IPCPL theory has a simple, clear empirical hypothesis: Private capital market transaction cost is a decreasing, convex function of the FMV, transaction price, or other variables directly influencing FMV or price. This means that IPCPL theory can easily be estimated and tested using common statistical methods if the variables implied by the hypothesis are observable.

IPCPL estimated from mid-market M&A data. Firmex is a provider of virtual data room and secure document sharing applications (see www.firmex.com) and has been conducting surveys of investment bankers and M&A advisors since 2016 with respect to mid-market M&A advisory fees. In particular, Firmex published survey results and data in the following documents:

Firmex, M&A Fee Guide 21/22: Key insights on M&A advisory fees in the middle market.

Firmex, M&A Fees Over the Years: A Fee Guide Companion (Trends in M&A advisory fees in the middle market from 2016 to 2020).

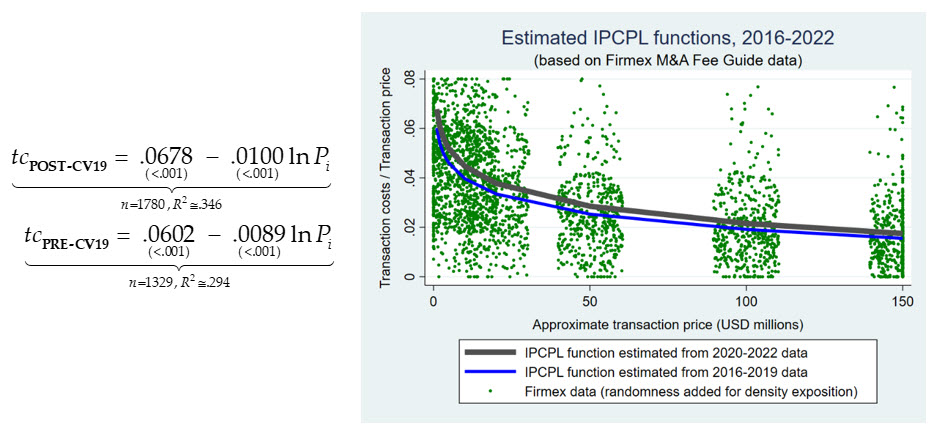
These documents provided data on approximate advisory fees as a percentage of transaction price (referred to as “success fee” in the documents) and approximate transaction price for 3109 transactions spanning the period 2016 through 2022, with 1329 transactions in the 2016–2019 period (referred to here as the pre-CV19 period) and 1780 in the 2020–2022 period (referred to here as the post-CV19 period). Using this data, the IPCPL model shown above in Equation (1), where , was estimated and tested separately for the pre-CV19 and post-CV19 periods:

The empirical results show: (i) signs of the model parameters are consistent with IPCPL theory and are reliably estimated (i.e., p-values reported below each parameter estimate is acceptable small), and (ii) the decreasing, convex shape of the estimated functions shown in the graphs are consistent with IPCPL theory.

The R² statistics shown below each of the estimated IPCPL models indicate that the models explain about 54 percent of the variation in tc_PRE-CV19 and 59 percent of the variation in tc_POST-CV19 (on a probability-weighted observation basis). Estimation of IPCPL models for subsets of the Firmex data—not reported here—suggest that significant portions of the variation not explained by the two models presented above are due to cross-border variations in M&A transaction costs. For example, such transaction costs were found to be somewhat higher in Brazil and somewhat lower in Europe, etc. Were a more complex model estimated controlling for such regional differences, estimated R² statistics would explain a significantly higher proportion of the variation in transaction costs reflected in the Firmex survey data.

3.4 Evaluation of Empirical Evidence

Both previously existing and new empirical evidence discussed above is quite consistent with the empirical predictions of IPCPL theory and, in our view, there is little or no reason to conclude that IPCPL theory is not valid or reliable. It is, however, the case that statistical results may not be consistent with intuition resulting from professional experience.

To test the extent to which the new empirical results above are consistent with professional intuition, consider the following example: We are developing a FMV estimate of a small enterprise located in the U.S. with an observed private market price of $500,000 circa 2022. Recalling the IPCPL models estimated in preceding system stated transaction price in millions of U.S. dollars (so, $500,000 = $.500 millions), expected transaction costs based on the post-CV19 model would be: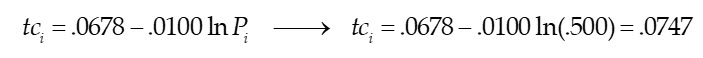

Because, however, there are typically legal and other professional fees associated with selling a business in addition to transaction advisory fees reflected in the Firmex data used to estimate the model, the estimate would reasonably be adjusted for such additional fees. We can make inquiries of attorneys and accountants, etc. on what their professional experience is with respect to the subject enterprise; and perhaps their responses suggest $25,000 ($.025 million) is a reasonable expectation of legal, accounting, and other professional fees associated with selling a business with a value approximating $500,000. In this case, the estimated all-in transaction costs based on the IPCPL model estimated above, augmented with an estimate of legal and other professional fees, would be: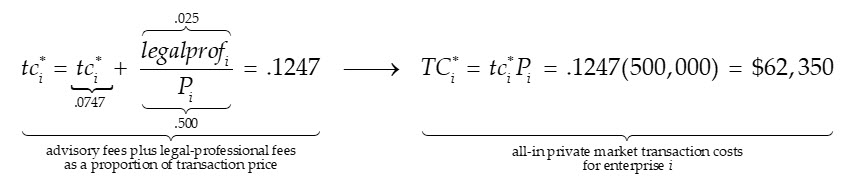

Based on our own experience in M&A transactions and on discussions with attorneys and accountants, this estimate appears intuitively reasonable.

Overall, we conclude that the available[1] empirical evidence is consistent with both IPCPL theory and professional experience and intuition.

3.5 Future Issue

In the final article in the series, Part IV, we will show how empirical evidence on IPCPL theory, such as that presented here, can be used in developing risk-adjusted discount rates adjusted for private capital market transaction costs consistent with IPCPL theory.

[1] It would be helpful if the owners of certain proprietary databases would allow their databases to be used for academic research.

---

David Goodman, MBA, CPA, CVA, has 25 years of experience in performing business valuations and forensic accounting services for family law and business disputes. He also has prepared business valuations for tax and buy-sell purposes. He has an MBA from the Amos Tuck School at Dartmouth College. He is a past-president of the NACVA-Mass State Chapter, past chair of the Massachusetts Society of Certified Public Accountants Litigation and BV committee, and a past board member and treasurer of the Massachusetts Collaborative Law Council. As a financial neutral, Mr. Goodman has helped divorcing couples reach peaceful equitable solutions. He has presented on business valuation and tax issues related to divorce at NACVA annual conference, NACVA-Mass. State Chapter, and the Massachusetts Collaborative Law Council. He has also testified as an expert witness in court and arbitration. He is currently serving on the editorial board of QuickRead.

Mr. Goodman can be contacted at (617) 698-3950 or by e-mail to dgoodman@joacpa.com.

Malcolm McLelland, PhD, has 40 years of professional and academic experience in finance and accounting, including positions in commercial banking, consulting, and educational institutions. His primary expertise is the use of econometric and financial modeling methods to assist clients with issues related to capital markets, financial reporting, and financial management. He has 15 years of international experience spanning client engagements in the United States, Brazil, and Southeast Asia. He has published in both academic and professional journals on finance and accounting topics, and has taught courses and presented seminars on finance- and accounting-related topics in major U.S. universities, Germany, and Latin America.

Dr. McLelland can be contacted by e-mail to mmc@mclelland-financial-economics.com.